PRML Figure6.5を再現するコード

これです。

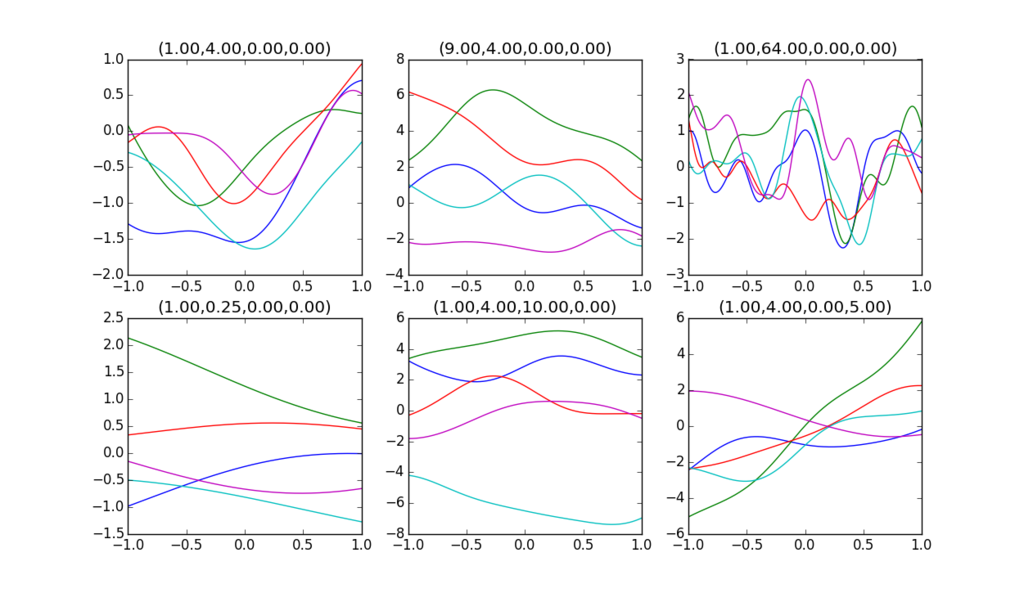
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal

params = [(1,4,0,0), (9,4,0,0), (1,64,0,0),
          (1,0.25,0,0), (1,4,10,0), (1,4,0,5)]

fig = plt.figure()
for n in range(len(params)):
  (p0, p1, p2, p3) = params[n]

  linex = np.linspace(-1,1,999)
  kern = np.zeros([len(linex),len(linex)])
  for i, x0 in enumerate(linex):
    for j, x1 in enumerate(linex):
      kern[i][j] = p0*np.exp(-p1*0.5*(x0-x1)*(x0-x1)) + p2 + p3*x0*x1
#      kern[i][j] = np.exp(-p1*0.5*np.abs(x0-x1))

  liney = multivariate_normal(np.zeros(len(linex)),kern,5)
  subplot = fig.add_subplot(2,3,n+1)
  subplot.set_title("(%1.2f,%1.2f,%1.2f,%1.2f)" % (p0,p1,p2,p3))
  for c in range(5):
    subplot.plot(linex, liney[c])

plt.show()

実行例

説明

連続なグラフとして描いていますが、実際には多数の離散点 $\{x_i\}_{i=1}^N$ に対して乱数で $y(x_i)$ の値を決定しています。この際、 $\{y(x_i)\}_{i=1}^N$ が N次元の多次元ガウス分布に従うという条件を設定しています。このような確率変数 $y(x_i)$ をガウス過程と呼びます。

多次元ガウス分布なので、平均と分散共分散行列を指定すれば一意に定まりますが、ここでは特に、カーネル関数を次で定義した上で、

　 $k(x_n,x_m) = \theta_0\exp\left\{-\frac{\theta_1}{2}(x_n-x_m)^2\right\} + \theta_2 + \theta_3 x_nx_m$

分散共分散行列を次式で決定しています。（平均は0に取ります。）

　 $C_{ij} = k(x_i,x_j)$

その上で、さまざまな $(\theta_0, \theta_1, \theta_2, \theta_3)$ に対してサンプルを取得したのが上記のグラフになります。

おまけ

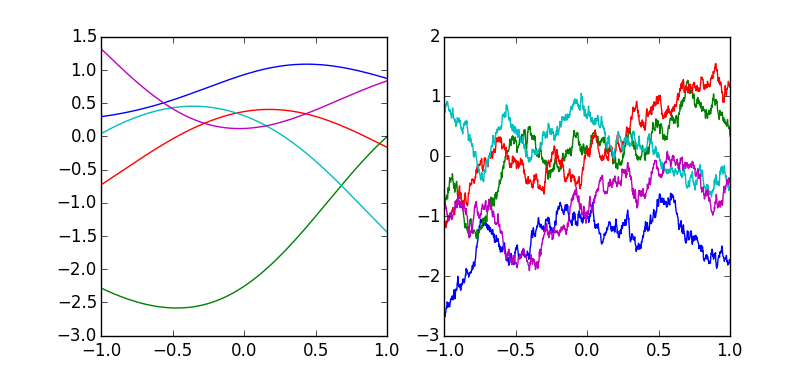
まったく同様に、Figure6.4は次のコードで再現できます。

import numpy as np
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal

fig = plt.figure()

# Gaussian Kernel
linex = np.linspace(-1,1,999)
kern = np.zeros([len(linex),len(linex)])
for i, x0 in enumerate(linex):
  for j, x1 in enumerate(linex):
    kern[i][j] = np.exp(-0.5*(x0-x1)*(x0-x1))
liney = multivariate_normal(np.zeros(len(linex)),kern,5)
subplot = fig.add_subplot(1,2,1)
for c in range(5):
  subplot.plot(linex, liney[c])

# Exponential Kernel
linex = np.linspace(-1,1,999)
kern = np.zeros([len(linex),len(linex)])
for i, x0 in enumerate(linex):
  for j, x1 in enumerate(linex):
      kern[i][j] = np.exp(-0.5*np.abs(x0-x1))

liney = multivariate_normal(np.zeros(len(linex)),kern,5)
subplot = fig.add_subplot(1,2,2)
for c in range(5):
  subplot.plot(linex, liney[c])

plt.show()