復習
上記の記事で見たように、次のように隠れユニットが2個あるニューラルネットワークを用いると、平面を2本の直線で分割する形での分類が可能になりました。
たとえば、次のような結果が得られます。
しかしながら、このモデルの場合、平面を4分割することはできても、4つの領域を任意に○✕に分類することはできません。たとえば、次のような「格子型」の配置は、うまく分類できません。
これはなぜかというと、隠れ層の出力は、 という4種類の値をとりますが、これを受け取るOutput層は
の一次関数の値で○✕を判定する必要があるためです。
平面に直線を一本引いて、領域を2つに分けた場合、「右上とその他」というような分類はできても、「(右上&左下)と(右下&左上)」というような分類はできないことがわかります。
この問題を解決するには、Output層もニューラルネットワーク化して、Output層の表現力を高めます。つまり、次のような2層構造のニューラルネットワークを組んであげます。
これで先ほどの「格子型」の問題にも対応可能になります。実際にサンプルコードで確認すると次のようになります。例よって、突貫で書いたので冗長ですが、関数single_layerと関数double_layerだけ見れば十分です。それぞれ、隠れ層が1つと2つのモデルによる計算を行っています。
from __future__ import absolute_import from __future__ import division from __future__ import print_function import tensorflow as tf import math import numpy as np from numpy.random import rand, multivariate_normal import matplotlib.pyplot as plt # dataset class Dataset(): def __init__(self): n1, n2, n3, n4 = 30, 30, 30, 30 mu1, mu2, mu3, mu4 = [-10,-10], [10,10], [-10, 10], [10,-10] cov1 = np.array([[10,0],[0,10]]) cov2 = np.array([[10,0],[0,10]]) cov3 = np.array([[10,0],[0,10]]) cov4 = np.array([[10,0],[0,10]]) data1 = multivariate_normal(mu1,cov1,n1) data2 = multivariate_normal(mu2,cov2,n2) data3 = multivariate_normal(mu3,cov3,n3) data4 = multivariate_normal(mu4,cov4,n4) data = np.r_[np.c_[data1,np.ones(n1)], np.c_[data2,np.ones(n2)], np.c_[data3,np.zeros(n3)], np.c_[data4,np.zeros(n4)]] np.random.shuffle(data) self.test_data, self.test_label = np.hsplit(data[0:20],[2]) self.train_data, self.train_label = np.hsplit(data[20:],[2]) self.index = 0 def next_batch(self, n): if self.index + n > len(self.train_data): self.index = 0 data = self.train_data[self.index:self.index+n] label = self.train_label[self.index:self.index+n] self.index += n return data, label def plot_result(sess, dataset, x, y, subplot1, subplot2, weight, bias, mult): data0_x, data0_y, data1_x, data1_y = [], [], [], [] for i in range(len(dataset.train_data)): if dataset.train_label[i][0] == 0: data0_x.append(dataset.train_data[i][0]) data0_y.append(dataset.train_data[i][1]) else: data1_x.append(dataset.train_data[i][0]) data1_y.append(dataset.train_data[i][1]) subplot1.scatter(data0_x, data0_y, marker='x', color='blue') subplot1.scatter(data1_x, data1_y, marker='o', color='blue') subplot2.scatter(data0_x, data0_y, marker='x', color='blue') subplot2.scatter(data1_x, data1_y, marker='o', color='blue') data0_x, data0_y, data1_x, data1_y = [], [], [], [] for i in range(len(dataset.test_data)): if dataset.test_label[i][0] == 0: data0_x.append(dataset.test_data[i][0]) data0_y.append(dataset.test_data[i][1]) else: data1_x.append(dataset.test_data[i][0]) data1_y.append(dataset.test_data[i][1]) subplot1.scatter(data0_x, data0_y, marker='x', color='red') subplot1.scatter(data1_x, data1_y, marker='o', color='red') subplot2.scatter(data0_x, data0_y, marker='x', color='red') subplot2.scatter(data1_x, data1_y, marker='o', color='red') xs, ys = np.hsplit(dataset.train_data,[1]) xmin, xmax = xs.min(), xs.max() ymin, ymax = ys.min(), ys.max() subplot1.set_ylim([ymin-1, ymax+1]) subplot1.set_xlim([xmin-1, xmax+1]) subplot2.set_ylim([ymin-1, ymax+1]) subplot2.set_xlim([xmin-1, xmax+1]) RES = 80 X = np.linspace(xmin-1,xmax+1,RES) Y = np.linspace(ymin-1,ymax+1,RES) field = [[xx,yy] for yy in Y for xx in X] a_k = y.eval(session=sess, feed_dict={x: field}) a_k = a_k.reshape(len(Y), len(X)) subplot1.imshow(np.sign(a_k-0.5), extent=(xmin-1,xmax+1,ymax+1,ymin-1), alpha=0.4) subplot2.imshow(a_k, extent=(xmin-1,xmax+1,ymax+1,ymin-1), alpha=0.4, vmin=0, vmax=1, cmap=plt.cm.gray_r) linex = np.arange(xmin-1, xmax+1) for i in range(len(bias[0])): wx, wy, b = weight[0][i], weight[1][i], bias[0][i] liney = - linex * wx/wy - b*mult/wy subplot2.plot(linex, liney, color='red') def single_layer(dataset, subplot1, subplot2): with tf.Graph().as_default(): mult = dataset.train_data.flatten().mean() hidden1_units = 2 # Create the model with tf.name_scope('input'): x = tf.placeholder(tf.float32, [None, 2]) with tf.name_scope('hidden1'): w1 = tf.Variable( tf.truncated_normal([2, hidden1_units],stddev=1.0/math.sqrt(2.0)), name='weights') b1 = tf.Variable(tf.zeros([1, hidden1_units]), name='biases') hidden1 = tf.nn.tanh(tf.matmul(x, w1) + b1*mult) # Logging data for TensorBoard _ = tf.histogram_summary('hidden1_weight', w1) _ = tf.histogram_summary('hidden1_bias', b1) with tf.name_scope('output'): w = tf.Variable(tf.zeros([hidden1_units,1]), name='weights') b = tf.Variable(tf.zeros([1]), name='biases') y = tf.nn.sigmoid(tf.matmul(hidden1, w) + b*mult) # Logging data for TensorBoard _ = tf.histogram_summary('output_weight', w) _ = tf.histogram_summary('output_bias', b) # Define loss and optimizer with tf.name_scope('optimizer'): y_ = tf.placeholder(tf.float32, [None, 1]) log_probability = tf.reduce_sum(y_*tf.log(y) + (1-y_)*tf.log(1-y)) train_step = tf.train.GradientDescentOptimizer(0.01).minimize(-log_probability) correct_prediction = tf.equal(tf.sign(y-0.5), tf.sign(y_-0.5)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # Logging data for TensorBoard _ = tf.histogram_summary('probability of training data', y) _ = tf.scalar_summary('log_probability', log_probability) _ = tf.scalar_summary('accuracy', accuracy) # Train with tf.Session() as sess: writer = tf.train.SummaryWriter('/tmp/nn_double', graph_def=sess.graph_def) sess.run(tf.initialize_all_variables()) for i in range(500): batch_xs, batch_ys = dataset.next_batch(100) feed = {x: batch_xs, y_: batch_ys} sess.run(train_step, feed_dict=feed) if i % 10 == 0: feed = {x: dataset.test_data, y_: dataset.test_label} summary_str, lp, acc = sess.run( [tf.merge_all_summaries(), log_probability, accuracy], feed_dict=feed) writer.add_summary(summary_str, i) print('LogProbability and Accuracy at step %s: %s, %s' % (i, lp, acc)) plot_result(sess, dataset, x, y, subplot1, subplot2, w1.eval(), b1.eval(), mult) def double_layer(dataset, subplot1, subplot2): with tf.Graph().as_default(): mult = dataset.train_data.flatten().mean() hidden1_units = 2 hidden2_units = 2 # Create the model with tf.name_scope('input'): x = tf.placeholder(tf.float32, [None, 2]) with tf.name_scope('hidden1'): w1 = tf.Variable( tf.truncated_normal([2, hidden1_units],stddev=1.0/math.sqrt(2.0)), name='weights') b1 = tf.Variable(tf.zeros([1, hidden1_units]), name='biases') hidden1 = tf.nn.tanh(tf.matmul(x, w1) + b1*mult) with tf.name_scope('hidden2'): w2 = tf.Variable( tf.truncated_normal([hidden1_units, hidden2_units], stddev=1.0/math.sqrt(2.0)), name='weights') b2 = tf.Variable(tf.zeros([1, hidden2_units]), name='biases') hidden2 = tf.nn.tanh(tf.matmul(hidden1, w2) + b2) # Logging data for TensorBoard _ = tf.histogram_summary('hidden1_weight', w1) _ = tf.histogram_summary('hidden1_bias', b1) _ = tf.histogram_summary('hidden2_weight', w2) _ = tf.histogram_summary('hidden2_bias', b2) with tf.name_scope('output'): w = tf.Variable(tf.zeros([hidden2_units,1]), name='weights') b = tf.Variable(tf.zeros([1]), name='biases') y = tf.nn.sigmoid(tf.matmul(hidden2, w) + b*mult) # Logging data for TensorBoard _ = tf.histogram_summary('output_weight', w) _ = tf.histogram_summary('output_bias', b) # Define loss and optimizer with tf.name_scope('optimizer'): y_ = tf.placeholder(tf.float32, [None, 1]) log_probability = tf.reduce_sum(y_*tf.log(y) + (1-y_)*tf.log(1-y)) train_step = tf.train.GradientDescentOptimizer(0.01).minimize(-log_probability) correct_prediction = tf.equal(tf.sign(y-0.5), tf.sign(y_-0.5)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # Logging data for TensorBoard _ = tf.histogram_summary('probability of training data', y) _ = tf.scalar_summary('log_probability', log_probability) _ = tf.scalar_summary('accuracy', accuracy) # Train with tf.Session() as sess: writer = tf.train.SummaryWriter('/tmp/nn_double', graph_def=sess.graph_def) sess.run(tf.initialize_all_variables()) for i in range(500): batch_xs, batch_ys = dataset.next_batch(100) feed = {x: batch_xs, y_: batch_ys} sess.run(train_step, feed_dict=feed) if i % 10 == 0: feed = {x: dataset.test_data, y_: dataset.test_label} summary_str, lp, acc = sess.run( [tf.merge_all_summaries(), log_probability, accuracy], feed_dict=feed) writer.add_summary(summary_str, i) print('LogProbability and Accuracy at step %s: %s, %s' % (i, lp, acc)) plot_result(sess, dataset, x, y, subplot1, subplot2, w1.eval(), b1.eval(), mult) # Main if __name__ == '__main__': fig = plt.figure() dataset = Dataset() subplot1 = fig.add_subplot(2,2,1) subplot2 = fig.add_subplot(2,2,2) single_layer(dataset, subplot1, subplot2) subplot1 = fig.add_subplot(2,2,3) subplot2 = fig.add_subplot(2,2,4) double_layer(dataset, subplot1, subplot2) plt.show()
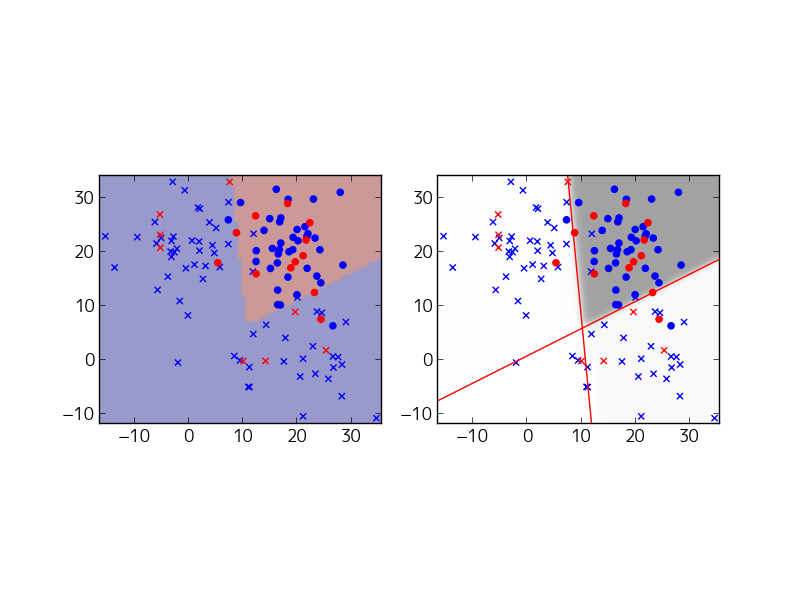
典型的な実行結果は、次のとおりです。(この問題は局所解があるので、綺麗な結果を得るには、何度か実行する必要があります。)
上の2つが隠れ層が1つのモデルで、予想通りうまくいきません。下の2つが隠れ層が2つのモデルで、予想通りにうまくいっています。右側の図の赤い直線は、1つめの隠れ層による平面の分割を示しています。
ちょっと休憩
今回のコードでは、対数尤度や正解率の計算を行う部分を「with tf.name_scope('optimizer')」というセクションに入れてあるので、TensorBoard上でのネットワークのグラフが次のように見やすくなっています。2層の隠れ層を持つことが一目で分かります。
「hidden1」の箱を開くと、中の詳細が確認できます。
特徴変数に基づいた分類ロジック
先ほどの結果にあるように、Output層にも隠れUnitを2つ入れることで、格子型の領域を分類できましたが、2つのUnitで分類できることがどうして分かるのでしょうか? 実はこれは、デジタル論理回路の設計と同じです。
上図を改めて見ると、左側は、AND計算(もしくは、OR計算)で判定していることになります。つまり、一次関数を内包した1つのUnitは、1つのAND(もしくはOR)回路と見なすことができます。一方、右側を正しく判定するには、XORの計算が必要ですので、1つのUnitでこの判定はできません。しかしながら!みなさんご存知のように3つのAND/OR回路を組み合わせることで、XORは表現可能です。つまり、先ほどの2層ニューラルネットワークは、次のように解釈できます。
これは次のように言い換えることもできます。オリジナルのデータは、2つの実数で表現されていますが、○✕という特徴を判定する上では、 というバイナリ変数で十分であり、このような特徴抽出を行うのが1つめの隠れ層です。そして、抽出した特徴に基づいて、○✕のマッピングを行うのが2つめの隠れ層以降になります。このように、オリジナルのデータから判定に必要な「特徴量」を取り出した変数
を「特徴変数」とも言います。「特徴変数の取り出し」+「特徴変数に基づいた分類」が多層ニューラルネットワークの本質と言ってもよいでしょう。
ちなみに、最近、「ニューラルネットワークってデジタル論理回路で実装できんじゃね?」という話題を耳にすることがあります。上記のモデルの場合、学習過程の計算は別にして、学習結果として得られる判定回路は、まさにデジタル論理回路であることが分かります。
次回予告
「TensorFlow Mechanics 101」で紹介されているサンプルコードでは、手書き文字分類を隠れ層が2層のニューラルネットワークで実施しており、今回の例と同様に「特徴変数の取り出し」+「特徴変数に基づいた分類」をモデル化したものと考えることができます。ただし、どのような特徴変数をつかえばよいかは、解くべき問題によって変わります。たとえば、画像分類の場合は、分類に役立つ「画像の特徴」を取り出す層を設計する必要があります。上記のサンプルコードでは、残念ながら手書き文字の特徴をうまく抽出できておらず、判定の正解率は、単なるロジスティック回帰(「TensorFlow Tutorialの数学的背景 − MNIST For ML Beginners(その2)」で紹介した、Output層のUnitだけを持つモデル)とほとんど変わりません。この次のステップとしては、画像の特徴抽出に古くから用いられてきた「畳込み演算」を隠れ層に組み入れることで、判定精度を向上していきます。これが、いわゆるCNN(Convolutional Neural Network/畳み込みニューラルネットワーク)の実体になります。
ちなみに、「ディープラーニングによって、特徴変数を考えなくてもよくなった!」という話を聞くこともありますが、適当にネットワークを組めば勝手に特徴変数を見つけてくれるわけではありません。適切な特徴変数が取り出せるようなネットワークの設計が必要となります。画像データに対しては、CNNがうまくいくということが経験的にわかっていますが、「どのようなデータに対してどのようなネットワークがよいのか」という一般論はまだよくわかっていません。与えられたデータに対して、最適なネットワークを発見するアルゴリズムを構成するような理論ができたらすごいのですが。。。。。
次の記事はこちらです。







