TensorFlow Tutorialの数学的背景 − MNIST For ML Beginners（その2）

enakai00.hatenablog.com

何の話かというと

上記の記事の続きです。

線形多項分類器

前回は、平面を2つの領域に分割しましたが、次のステップとして、3つ以上の領域に分類する方法を考えます。色々な方法が考えられますが、ここでは、前回同様に一次関数を用いて分類する方法を用います。たとえば、3つに分類する場合、前回の $f(x_0, x_1)$ と同様の関数を3つ用意します。

　 $f_1(x_0,x_1) = w_{01}x_0+w_{11}x_1+b_1$

　 $f_2(x_0,x_1) = w_{02}x_0+w_{12}x_1+b_2$

　 $f_3(x_0,x_1) = w_{03}x_0+w_{13}x_1+b_3$

そして、ある点 $(x_0,x_1)$ に対して、 $f_1$ 〜 $f_3$ の中で値が最も大きくなるものでこの点の分類を決めます。たとえば、 $f_2$ が最大だった場合、この点は「グループ2」に属するという具合です。

これは、図形的には次のように理解できます。あえて言葉で説明するので、その様子を頭の中で想像してください。

まず、 $(x_0,x_1)$ 平面に縦方向の軸を追加して、関数 $f_1(x_0,x_1)$ の値をグラフに描くと、 $(x_0,x_1)$ 平面に対して、傾いた板が配置される形になります。 $(x_0,x_1)$ 平面と「傾いた板」が交わる直線が $f_1(x_0,x_1)=0$ に対応します。

それでは、同じことを $f_2(x_0,x_1)$ 、 $f_3(x_0,x_1)$ についても行うと、どうなるでしょうか？ ―― それぞれ異なる方向に傾いた3枚の板が、お互いに突き刺さりながら配置される様子が想像できるのではないでしょうか？

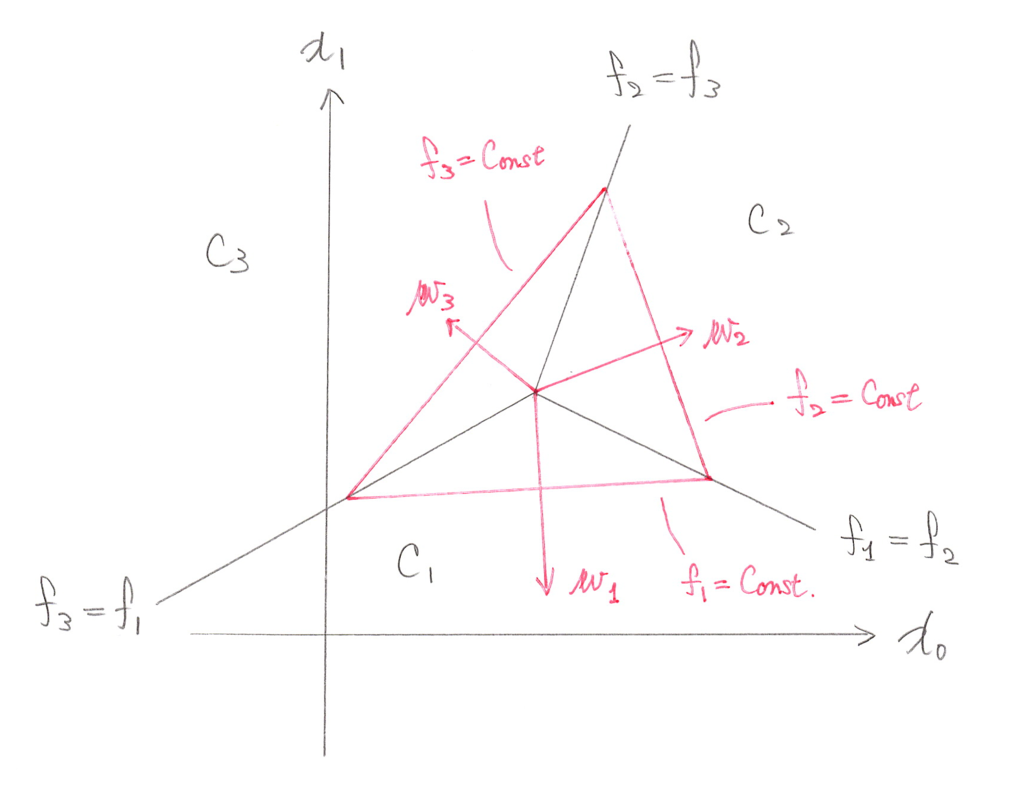
この時、よーーーく考えると、（傾きの方向がバラバラだとすると）3枚の板は必ずある1点で交わります。数学的に言うと、連立方程式 $f_1=f_2, f_1=f_3$ は必ず解 $(x_0,x_1)$ を1つ持つことからも分かります。この点に注意して、 $(x_0,x_1)$ 平面上に3つの領域の境界線、すなわち、 $f_1=f_2$ 、 $f_2=f_3$ 、 $f_3=f_1$ で決まる直線を描くと次のようになります。

$C_1,C_2,C_3$ が分割された3つの領域です。赤いベクトル ${\mathbf w}_1,{\mathbf w}_2,{\mathbf w}_3$ は、 $f_1, f_2, f_3$ の値が増加する方向（傾いた板を登っていく方法）で、赤い三角形は「等高線」に相当します。

この方法により、任意の個数の領域に分割できることがわかりますが、4個以上に分割する場合は、すべての領域が1点で接触するとは限りません。たとえば、次のような例が考えられます。

　 $f_1=x_0,\,\,f_2=x_1,\,\,f_3=-0.1(x_0+x_1),\,\,f_4=-3(x_0+x_1)-3$

最後に $f_1, f_2,\cdots$ の値を確率に変換する方法を考えます。先程は、一番値が大きい $f_i$ で領域が決まるといいましたが、 $f_1, f_2,\cdots$ の大きさは、その点が対応する領域に属する「確率」に対応するものとします。つまり、 $f_i$ の値が大きいほど、その点が i 番目の領域である確率が高いものと考えます。そのためには、 $f_i$ の値を 0 〜 1 の範囲に変換して、かつ、それぞれの領域である確率の合計が 1 になるように調整する必要があります。これは、次の「softmax関数」で実現できます。

　 $P_i(x_0,x_1) = e^{f_i(x_0,x_1)}/\sum_{k=1}^{K}e^{f_k(x_0,x_1)}$

ここでは、全部で K 個の領域に分割するものと想定しており、点 $(x_0,x_1)$ が i 番目の領域である確率が $P_i(x_0,x_1)$ で与えられます。

手書き文字画像の分類

それでは、いよいよ手書き文字画像の分類に入ります。使用するデータは下記のような画像で、1つの文字は28x28ピクセル（合計784ピクセル）あり、それぞれのピクセルには色の濃さを表す数値が振られています。

つまり、1つの文字は、784個の数値の組で表現されており、これらの数値を一列に並べた784次元ベクトルとして表すことができます。言い換えると、1つの文字は、784次元空間の1つの点に対応します。同じ数字を表す文字は、784次元空間の中で互いに近い場所に集まるものと期待することができます。

そこで、先ほどの手法を用いて、784次元空間を「0」〜「9」の数字に対応する10個の場所に分類します。これは（ $m=783$ として）関数 $f_i(x_0,\cdots,x_m)$ を10個用意することで実現できます。行列形式でまとめて書くと、次のようになります。

　 $(f_0,\cdots,f_9) = (x_0,\cdots,x_m) \left( \begin{array}{rr} w_{00} & w_{01} & \cdots & w_{09} \\ w_{10} & w_{11} & \cdots & w_{19} \\ \vdots \\ w_{m0} & w_{m1} & \cdots & w_{m9}\\ \end{array} \right)+ (b_0,\cdots,b_9)$ ―― (0)

さらに、softmax関数を用いて確率に変換します。 ${\mathbf x}=(x_0,\cdots,x_m)$ として、次のようになります。

　 $P_i({\mathbf x}) = e^{f_i({\mathbf x})} / \sum_{k=0}^9 e^{f_k({\mathbf x})}$ 　（ $i=0,\cdots,9$ ）

そして、この確率を用いてトレーニングセットのデータが得られる確率を計算するわけですが、計算上の工夫のために、n 番目のデータの実際の数字が k だったとして、これを次のベクトルで表現します。

　 ${\mathbf t_n} = (0,\cdots,1,\cdots,0)$ （k+1 番目の数字のみ 1 になっているベクトル）

この記法を用いると、トレーニングセットのデータ $\left\{({\mathbf x_n}, {\mathbf t}_n)\right\}_{n=1}^N$ が得られる確率は次になります。

　 $P = \prod_{n=1}^N\prod_{k=0}^9 \left\{e^{f_k({\mathbf x_n})} / \sum_{k'=0}^9 e^{f_{k'}({\mathbf x_n})}\right\}^{t_{nk}}$

ここに、 $t_{nk}$ は ${\mathbf t}_n$ の k 番目の要素を表します。少し複雑に見えますが、

　 $y_{nk} = e^{f_k({\mathbf x_n})} / \sum_{k'=0}^9 e^{f_{k'}({\mathbf x_n})}$ ―― (1)

と置くとシンプルになります。

　 $P = \prod_{n=1}^N\prod_{k=0}^9 y_{nk}^{t_{nk}}$

ここまでくれば、準備はほぼできました。この確率を最大にするために、次の対数尤度関数を最大化するアルゴリズムを適用します。

　 $\log P = \sum_{n=1}^N\sum_{k=0}^9t_{nk}\log y_{nk}$ ―― (2)

(2)の符号違い（ $-\log P$ ）は、統計学の用語で「クロスエントロピー」と呼ばれるものになっています。

(1)(2)は、ちょうど、前回の記事の(1)(2)に対応するものになっています。次元数が増えただけで、本質的にやっていることは同じです。あとは、TensorFlowに組み込みのアルゴリズムで、(2)を最大にするパラメーター $w_{ij}, b_j$ を決定するだけです。

コードの解説

ここでは、TensorBoard用のデータ出力などを省略した、一番シンプルなコードを使って解説します。

・mnist_softmax.py

まず、(1)の定義は次の部分です。

# Create the model
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x, W) + b)

x がトレーニングセットのデータを注入する placeholder です。784個の要素を持つベクトルがN個あるとして、(Nx784)行列になります。実際には N は不定なので、None が指定されています。

W は係数 $w_{ij}$ の行列で、先ほどの(0)の表式から分かるように、(784x10)行列です。b は定数項 $b_j$ で、(1x10)行列です。

最後に y が、(1)の定義に対応します。組み込みの softmax() 関数を使用しています。

続いて、(2)のクロスエントロピーの定義です。

# Define loss and optimizer
y_ = tf.placeholder(tf.float32, [None, 10])
cross_entropy = -tf.reduce_sum(y_ * tf.log(y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

y_ は、トレーニングセットのラベル ${\mathbf t}$ を縦に積み上げた (Nx10)行列で、cross_entropy がそのまま(2)の符号違いに対応していることが分かります。tf.log()は行列を代入すると各成分にlog()が演算されて、行列と行列の掛け算(*)は、各成分の掛け算になります。reduce_sum()は、行列のすべての要素を足しあげる関数で、 $\sum_{n=1}^N\sum_{k=0}^9$ の計算に対応します。

train_stepは、cross_entropyを最小化するように変数を調整するアルゴリズムの指定です。

アルゴリズムの実行は下記の部分です。

# Train
tf.initialize_all_variables().run()
for i in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  train_step.run({x: batch_xs, y_: batch_ys})

トレーニングセットのデータを10個づつ取り出して、アルゴリズムに放り込んで変数を調整していきます。前回のサンプルと少し形式が違いますが、次の2つは同じ処理内容になります。

train_step.run({x: batch_xs, y_: batch_ys})

sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

トレーニングのループが終わったら、テストデータに対する正解率を計算して表示します。

# Test trained model
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(accuracy.eval({x: mnist.test.images, y_: mnist.test.labels}))

argmax(y,1) は、行列 y を横方向にみて最大値を与えるインデックスを返す関数です。（2つ目の引数「1」は横方向を意味します。）softmax関数で得られた確率の最も大きいクラスに属するものと判定しています。

次回予告

ここまで、TensorFlowを使いながら、ニューラルネットワークは一切出てきませんでした。が・・・・ニューラルネットワークを用いた場合でも、数学的な本質は変わりません。今回の例では、一次関数 $f_i$ を用いて空間を直線的に分割していましたが、この関数をより複雑にすることで、より複雑な分類が可能になります。関数 $f_i$ の代わりにニューラルネットワークで値を算出して、最後にそれをsoftmax関数にぶちこんで、どのクラスに属するかを判定する、というのが次のステップになります。

次の記事はこちらです。

enakai00.hatenablog.com