TensorFlow Tutorialの数学的背景 − TensorFlow Mechanics 101（その1）

何の話かというと

まず、下記の記事では、2次元平面を直線（一次関数）で分類するという問題を解きました。

enakai00.hatenablog.com

続いて、下記の記事では、2次元平面を多次元空間に拡張することで、手書き文字の分類ができることを示しました。これは、TensorFlow Tutorialの最初に登場する「MNIST For ML Beginners」と同じ処理にあたります。

enakai00.hatenablog.com

そして、TensorFlow Tutorialの下記の例では、次のステップとして、「一次関数をニューラルネットワークに置き換える」という拡張を行っています。

・TensorFlow Mechanics 101

ここでは類似の拡張を２次元平面の分類問題に適用することで、ニューラルネットワークの本質をわかりやすく解説していきます。

問題設定

冒頭の記事では、いかにも直線で分類できそうなデータを用意しましたが、いつでも直線だけでうまくいくとは限りません。たとえば、下記のように、折れ曲がった線でないとうまく分類できない場合もあります。

これは、分類に使用する関数を一次関数ではなくて、もっと複雑な曲線の関数に置き換えればよいだけの事なのですが、具体的にどのような関数がよいのかは、最初からはなかなかわかりません。そこで、普段よく使う関数の代わりに、ニューラルネットワークによる計算で置き換えようというのが、ここでの発想です。

下記は、最もシンプルなニューラルネットワークの例で、「隠れ層」と呼ばれるユニット（隠れUnit）が2つあります。

2つの隠れUnitは、座標 $(x_0, x_1)$ を入力すると、次の関数で値を1つ出力します。

　 $z_0 = \tanh(w_{00} x_0 + w_{10} x_1 + b_0)$ ―― (1)

　 $z_1 = \tanh(w_{01} x_0 + w_{11} x_1 + b_1)$ ―― (2)

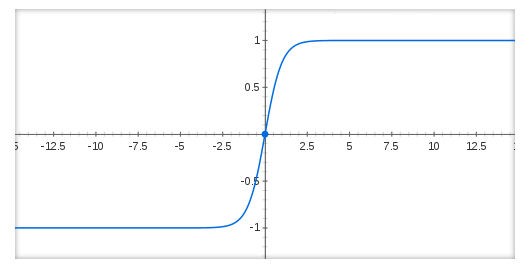
$\tanh$ は、下図のように、原点付近で-1から1にひょこっと値が立ち上がる関数です。

つまり、一次関数 $w_{00} x_0 + w_{10} x_1 + b_0$ 、および、 $w_{01} x_0 + w_{11} x_1 + b_1$ の値の符号によって、-1か1を出力する関数になります。（厳密には、-1から1に不連続に変化するわけではありませんが、本質的には、-1か1を取ると思って大丈夫です。）入力値の変化によって、ユニットの出力が-1から1に変化する様子が、ニューロン（脳神経細胞）がピクッと反応する様子ににているので、これを表現する関数 $\tanh$ を「Activation」と呼ぶこともあります。

さらに、最後の出力ユニット（Output Unit）は、隠れ層からの出力を受け取って、シグモイド関数で0〜1の値を出力します。

　 $y = \sigma(w_0 z_0 + w_1 z_1 + b)$ ―― (3)

結論としては、これまで、

　 $y = \sigma(w_0 x_0 + w_1 x_1 +b)$

というように、シグモイド関数の入力に一次関数を用いていた部分を (1)〜(3) で定義される関数に置き換えることになります。この後は、最尤推定法に従って、対数尤度：

　 $\log P = \sum_i \left\{t_i\log y_i + (1-t_i)\log (1-y_i)\right\}$

を最大にするようにパラメーター $w_{00},w_{10},w_{01},w_{11},b_{0},b_{1},w_0,w_1,b$ を調整すれば答えが得られます。

ニューラルネットワークが表現する関数

それでは、(1)〜(3)で表現される関数は、実際のところ、どのような関数なのでしょうか？　実は、この例の場合はそれほど複雑ではありません。それぞれの隠れUnitは、一次関数の符号によって、±1を出力しました。そして、この一次関数は平面を分割する直線になります。結局、1つの隠れUnitは、平面を直線で分割して、その両側で±1 を出力することになります。今の場合、隠れUnitが2つありますので、 $(x_0,x_1)$ 平面は、2本の直線で4つの領域に分割されます。それぞれの領域に対して、 $(z_0,z_1) = (-1,-1),(1,-1),(-1,1),(1,1)$ という4種類の値が、出力Unitに入ります。

最後に出力Unitは、この4種類の入力に対して、○の領域である確率を計算します。つまり、平面上の4つの領域がそれぞれ、○か✕かに分離されることになります。

コードで確認

突貫で書いたのできれいではありませんが、TensorFlowを用いると、上記のニューラルネットワークはこんなコードで実装できます。例によって、「# Main」以下だけ見れば十分です。その他は、データの生成とグラフの描画部分です。

nn_regression.py

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import tensorflow as tf
import math
import numpy as np
from numpy.random import rand, multivariate_normal
import matplotlib.pyplot as plt

# dataset
class Dataset():
  def __init__(self):
    variance = 40
    n1, n2, n3 = 50, 40, 30
    mu1, mu2, mu3 = [20,20], [0,20], [20, 0]
    cov1 = np.array([[variance,0],[0,variance]])
    cov2 = np.array([[variance,0],[0,variance]])
    cov3 = np.array([[variance,0],[0,variance]])
    data1 = multivariate_normal(mu1,cov1,n1)
    data2 = multivariate_normal(mu2,cov2,n2)
    data3 = multivariate_normal(mu3,cov3,n3)
    data = np.r_[np.c_[data1,np.ones(n1)],
                 np.c_[data2,np.zeros(n2)],
                 np.c_[data3,np.zeros(n3)]]
    np.random.shuffle(data)

    self.test_data, self.test_label = np.hsplit(data[0:20],[2])
    self.train_data, self.train_label = np.hsplit(data[20:],[2])
    self.index = 0

  def next_batch(self, n):
    if self.index + n > len(self.train_data):
        self.index = 0
    data = self.train_data[self.index:self.index+n]
    label = self.train_label[self.index:self.index+n]
    self.index += n
    return data, label

def plot_result(dataset, x, y, weight, bias, mult):
  fig = plt.figure()
  subplot1 = fig.add_subplot(1,2,1)
  subplot2 = fig.add_subplot(1,2,2)

  data0_x, data0_y, data1_x, data1_y = [], [], [], []
  for i in range(len(dataset.train_data)):
    if dataset.train_label[i][0] == 0:
      data0_x.append(dataset.train_data[i][0])
      data0_y.append(dataset.train_data[i][1])
    else:
      data1_x.append(dataset.train_data[i][0])
      data1_y.append(dataset.train_data[i][1])
  subplot1.scatter(data0_x, data0_y, marker='x', color='blue')
  subplot1.scatter(data1_x, data1_y, marker='o', color='blue')
  subplot2.scatter(data0_x, data0_y, marker='x', color='blue')
  subplot2.scatter(data1_x, data1_y, marker='o', color='blue')

  data0_x, data0_y, data1_x, data1_y = [], [], [], []
  for i in range(len(dataset.test_data)):
    if dataset.test_label[i][0] == 0:
      data0_x.append(dataset.test_data[i][0])
      data0_y.append(dataset.test_data[i][1])
    else:
      data1_x.append(dataset.test_data[i][0])
      data1_y.append(dataset.test_data[i][1])
  subplot1.scatter(data0_x, data0_y, marker='x', color='red')
  subplot1.scatter(data1_x, data1_y, marker='o', color='red')
  subplot2.scatter(data0_x, data0_y, marker='x', color='red')
  subplot2.scatter(data1_x, data1_y, marker='o', color='red')

  xs, ys = np.hsplit(dataset.train_data,[1])
  xmin, xmax = xs.min(), xs.max()
  ymin, ymax = ys.min(), ys.max()
  subplot1.set_ylim([ymin-1, ymax+1])
  subplot1.set_xlim([xmin-1, xmax+1])
  subplot2.set_ylim([ymin-1, ymax+1])
  subplot2.set_xlim([xmin-1, xmax+1])

  RES = 80
  X = np.linspace(xmin-1,xmax+1,RES)
  Y = np.linspace(ymin-1,ymax+1,RES)
  field = [[xx,yy] for yy in Y for xx in X]
  a_k = y.eval(session=sess, feed_dict={x: field})
  a_k = a_k.reshape(len(Y), len(X))
  subplot1.imshow(np.sign(a_k-0.5), extent=(xmin-1,xmax+1,ymax+1,ymin-1),
                  alpha=0.4)
  subplot2.imshow(a_k, extent=(xmin-1,xmax+1,ymax+1,ymin-1),
                  alpha=0.4, vmin=0, vmax=1, cmap=plt.cm.gray_r)

  linex = np.arange(xmin-1, xmax+1)
  for i in range(len(bias[0])):
    wx, wy, b = weight[0][i], weight[1][i], bias[0][i]
    liney = - linex * wx/wy - b*mult/wy
    subplot2.plot(linex, liney, color='red')
  plt.show()

# Main
if __name__ == '__main__':

  with tf.Graph().as_default():
    dataset = Dataset()
    mult = dataset.train_data.flatten().mean()
    hidden1_units = 2
    
    # Create the model
    with tf.name_scope('input'):
      x = tf.placeholder(tf.float32, [None, 2])
  
    with tf.name_scope('hidden1'):
      w0 = tf.Variable(
        tf.truncated_normal([2, hidden1_units],stddev=1.0/math.sqrt(2.0)),
        name='weights')
      b0 = tf.Variable(tf.zeros([1, hidden1_units]), name='biases')
  #    hidden1 = tf.nn.relu(tf.matmul(x, w0) + b0*mult)
      hidden1 = tf.nn.tanh(tf.matmul(x, w0) + b0*mult)
  
      # Logging data for TensorBoard
      _ = tf.histogram_summary('hidden_weight', w0)
      _ = tf.histogram_summary('hidden_bias', b0)
  
    with tf.name_scope('output'):
      w = tf.Variable(tf.zeros([hidden1_units,1]), name='weights')
      b = tf.Variable(tf.zeros([1]), name='biases')
      y = tf.nn.sigmoid(tf.matmul(hidden1, w) + b*mult)
  
      # Logging data for TensorBoard
      _ = tf.histogram_summary('output_weight', w)
      _ = tf.histogram_summary('output_bias', b)
  
    # Define loss and optimizer
    y_ = tf.placeholder(tf.float32, [None, 1])
    log_probability = tf.reduce_sum(y_*tf.log(y) + (1-y_)*tf.log(1-y))
    train_step = tf.train.GradientDescentOptimizer(0.001).minimize(-log_probability)
    correct_prediction = tf.equal(tf.sign(y-0.5), tf.sign(y_-0.5))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    
    # Logging data for TensorBoard
    _ = tf.histogram_summary('probability of training data', y)
    _ = tf.scalar_summary('log_probability', log_probability)
    _ = tf.scalar_summary('accuracy', accuracy)
    
    # Train
    with tf.Session() as sess:
      writer = tf.train.SummaryWriter('/tmp/nn_logs', graph_def=sess.graph_def)
      sess.run(tf.initialize_all_variables())
      for i in range(500):
        batch_xs, batch_ys = dataset.next_batch(100)
        feed = {x: batch_xs, y_: batch_ys}
        sess.run(train_step, feed_dict=feed)
      
        feed = {x: dataset.test_data, y_: dataset.test_label}
        summary_str, lp, acc = sess.run(
          [tf.merge_all_summaries(), log_probability, accuracy], feed_dict=feed)
        writer.add_summary(summary_str, i)
        print('LogProbability and Accuracy at step %s: %s, %s' % (i, lp, acc))
    
      plot_result(dataset, x, y, w0.eval(), b0.eval(), mult)

先に実行結果を示すと、次のようになります。

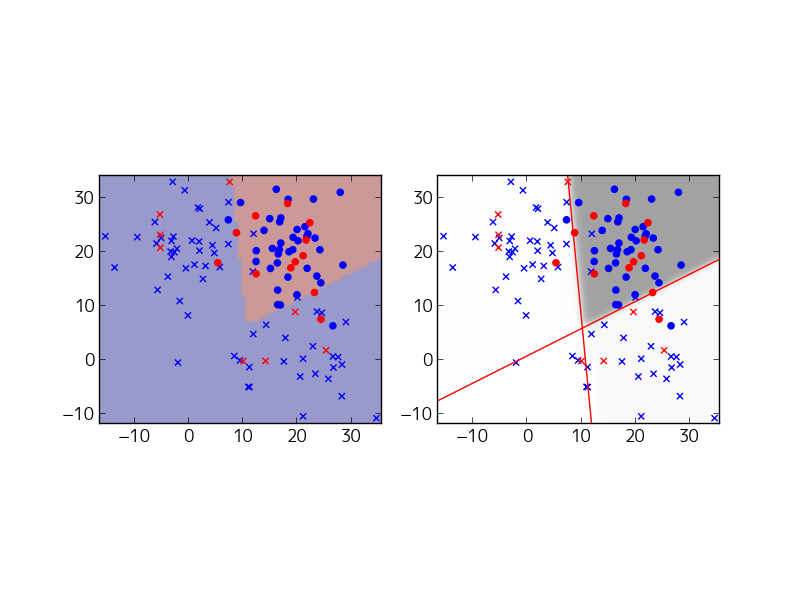
左側は、出力Unitの値が0.5以上／以下で色分けしたもので、○である確率が0.5以上の所を○の領域と判断しています。一方、右側は、隠れUnitの $\tanh$ に入力される一次関数で決まる直線を引いてあります。2本の直線で空間が4つに分類されていることがよく分かります。また、右側の図は、平面上の各点における出力Unitの値を白黒の濃淡で示しています。直線の境界部分で、白から黒になめらかに変化していることが読み取れます。

続いて、コードのポイントを示しておきます。まず、入力層を定義します。

    # Create the model
    with tf.name_scope('input'):
      x = tf.placeholder(tf.float32, [None, 2])

ここでは、トレーニングセットのデータ $(x_0,x_1)$ を縦にならべた行列を受け取るplaceholderとして、xを定義しています。"with tf.name_scope('input'):" は、TensorBoradでネットワークのグラフを描くときに、関連する変数を1つの箱にまとめて表示するためのスコープ指定です。ここでは、入力層の箱を用意して、その中に変数 x を入れるようにしています。

次は、隠れ層を定義します。

    with tf.name_scope('hidden1'):
      w0 = tf.Variable(
        tf.truncated_normal([2, hidden1_units],stddev=1.0/math.sqrt(2.0)),
        name='weights')
      b0 = tf.Variable(tf.zeros([1, hidden1_units]), name='biases')
      hidden1 = tf.nn.tanh(tf.matmul(x, w0) + b0*mult)

w0とb0は、(1)(2)に現れる係数をまとめた行列です。hidden1_unitsは隠れUnitの個数で、ここでは2になっています。hidden1は、(1)(2)の計算結果となる $(z_0,z_1)$ を（トレーニングセットからの入力値に対応して）縦にならべた行列になります。Variableの定義につけたnameは、TendorBoardで表示するときの名前の指定です。

最後に出力層の定義です。

    with tf.name_scope('output'):
      w = tf.Variable(tf.zeros([hidden1_units,1]), name='weights')
      b = tf.Variable(tf.zeros([1]), name='biases')
      y = tf.nn.sigmoid(tf.matmul(hidden1, w) + b*mult)

これは、(3)の計算に対応します。

これでニューラルネットワークが定義できました。ここから先の処理は、「TensorFlow Tutorialの数学的背景 − MNIST For ML Beginners（その1）」とまったく同じです。何度も言いますが、一次関数をニューラルネットワークに置き換えただけで、数学的にやっていることはこれまでと同じです。

まず、対数尤度を定義して、それを最大化するアルゴリズムを指定します。

    # Define loss and optimizer
    y_ = tf.placeholder(tf.float32, [None, 1])
    log_probability = tf.reduce_sum(y_*tf.log(y) + (1-y_)*tf.log(1-y))
    train_step = tf.train.GradientDescentOptimizer(0.001).minimize(-log_probability)
    correct_prediction = tf.equal(tf.sign(y-0.5), tf.sign(y_-0.5))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

アルゴリズムを適用して、実際に計算を行います。

    # Train
    with tf.Session() as sess:
      writer = tf.train.SummaryWriter('/tmp/nn_logs', graph_def=sess.graph_def)
      sess.run(tf.initialize_all_variables())
      for i in range(500):
        batch_xs, batch_ys = dataset.next_batch(100)
        feed = {x: batch_xs, y_: batch_ys}
        sess.run(train_step, feed_dict=feed)

ここでは、100個あるトレーニングデータを全部まとめてsess.run()にほり込んで計算する、ということを500回繰り返しています。実際に計算してみると、関数が複雑になっている分、計算回数を増やさないとなかなか最適な値に到達しないことが分かります。

参考までに、TensorBoardで表示した学習曲線を示しておきます。

accuracyは、テストデータに対する正解率ですが、何度も計算を繰り返していると、突然、あるタイミングで高い正解率で安定することが分かります。確率的にパラメーターを振って最適な値を探していくアルゴリズムなので、こういうことが起こっているものと想像されます。

もうひとつおまけで、TensorBoradから見えるニューラルネットワークの全体像です。

赤丸の部分がコード内で定義した入力層、隠れ層、出力層になります。その周りに広がっているのは、対数尤度や正解率を計算するためのグラフと思われます。ニューラルネットワークのパラメーターを最適化する際は、このようなネットワークを逆向きにたどっていくBack Propagationを構成して計算する必要がありますが、TensorFlowは、そこらへんの計算を勝手にやってくれるわけです。