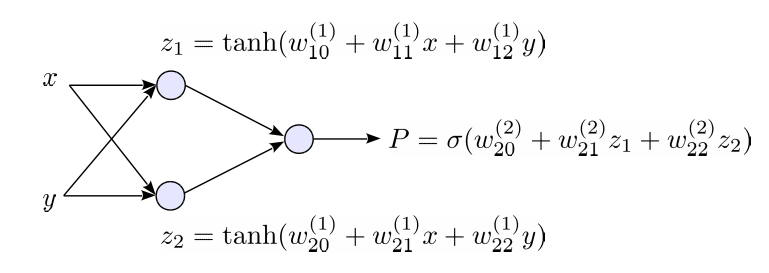やる事
(x, y) 平面上のデータをロジスティクス回帰で二項分類します。
回帰式として、中間層に2個のユニットを持つ下記のNeural Networkを使用します。バイアス項を含めて、9個のパラメーター を持つ関数になります。
次の誤差関数を極小にするように、Back Propagationでパラメーターを最適化します。(最尤推定に相当します。)
PRMLのFigure 5.4に相当する処理になります。
これをPythonでベタに実装すると次のコードになります。
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt import pandas as pd from pandas import Series, DataFrame from numpy.random import multivariate_normal, rand N1 = 10 Mu1 = [40,10] N2 = 10 Mu2 = [10,-10] N3 = 15 Mu3 = [5,8] def sigmoid(a): return 1.0/(1.0+np.exp(-a)) def prepare_dataset(): cov1 = np.array([[30,0],[0,80]]) cov2 = np.array([[80,0],[0,10]]) cov3 = np.array([[60,0],[0,20]]) df1 = DataFrame(multivariate_normal(Mu1,cov1,N1),columns=['x','y']) df1['type'] = 1 df2 = DataFrame(multivariate_normal(Mu2,cov2,N2),columns=['x','y']) df2['type'] = 1 df3 = DataFrame(multivariate_normal(Mu3,cov3,N3),columns=['x','y']) df3['type'] = 0 df = pd.concat([df1,df2,df3],ignore_index=True) df = df.reindex(np.random.permutation(df.index)).reset_index() return df[['x','y','type']] def run_simulation(tset, M, subplot1, subplot2): tset1 = tset[tset['type']==1] tset2 = tset[tset['type']==0] ymin, ymax = tset.y.min()-5, tset.y.max()+10 xmin, xmax = tset.x.min()-5, tset.x.max()+10 bias = 0.5 * (tset.x.mean() + tset.y.mean()) w = {} def f(x,y): a = [0.0]*M z = [0.0]*M for j in range(1,M): a[j] = w[(1,(j,0))]*bias + w[(1,(j,1))]*x + w[(1,(j,2))]*y z[j] = np.tanh(a[j]) a_k = w[(2,(1,0))]*1.0 for j in range(1,M): a_k += w[(2,(1,j))]*z[j] return a_k, a def initval(): return rand()-0.5 w[(2,(1,0))]=initval() for j in range(1,M): w[(1,(j,0))] = initval() w[(1,(j,1))] = initval() w[(1,(j,2))] = initval() w[(2,(1,j))] = initval() eta = 0.05 err_pre = 10000 for iter_num in range(1000): for index, point in tset.iterrows(): x, y, type = point.x, point.y, point.type a_k, a = f(x,y) d_k = sigmoid(a_k) - type w[(2,(1,0))] -= eta * d_k * 1 d = [0] * M for j in range(1,M): d[j] = d_k*w[(2,(1,j))]*(1.0-np.tanh(a[j])*np.tanh(a[j])) w[(1,(j,0))] -= eta * d[j] * bias w[(1,(j,1))] -= eta * d[j] * x w[(1,(j,2))] -= eta * d[j] * y w[(2,(1,j))] -= eta * d_k * np.tanh(a[j]) err = 0 for index, point in tset.iterrows(): x, y, type = point.x, point.y, point.type a_k, a = f(x,y) p = sigmoid(a_k) err += -(type*np.log(p)+(1-type)*np.log(1.0-p)) if np.abs(err_pre - err) < err_pre * 0.00001: print "break" break err_pre = err print err_pre RES = 80 X = np.linspace(xmin,xmax,RES) Y = np.linspace(ymin,ymax,RES) field1 = DataFrame(np.zeros(shape=(len(X),len(Y)))) field2 = DataFrame(np.zeros(shape=(len(X),len(Y)))) for x, xval in enumerate(X): for y, yval in enumerate(Y): a_k, a = f(xval,yval) field1.ix[y,x] = np.sign(sigmoid(a_k)-0.5) field2.ix[y,x] = sigmoid(a_k) subplot1.set_title('M=%d, Err=%1.2f' % (M-1, err_pre)) subplot1.set_xticks([]) subplot1.set_yticks([]) subplot1.set_ylim([ymin-1, ymax+1]) subplot1.set_xlim([xmin-1, xmax+1]) subplot1.scatter(tset1.x, tset1.y, marker='o') subplot1.scatter(tset2.x, tset2.y, marker='x') subplot1.imshow(field1.values, extent=(xmin,xmax,ymax,ymin), alpha=0.4) subplot2.set_title('M=%d, Err=%1.2f' % (M-1, err_pre)) subplot2.set_xticks([]) subplot2.set_yticks([]) subplot2.set_ylim([ymin-1, ymax+1]) subplot2.set_xlim([xmin-1, xmax+1]) subplot2.scatter(tset1.x, tset1.y, marker='o') subplot2.scatter(tset2.x, tset2.y, marker='x') subplot2.imshow(field2.values, extent=(xmin,xmax,ymax,ymin), alpha=0.4, vmin=0, vmax=1, cmap=plt.cm.gray_r) # Main if __name__ == '__main__': fig = plt.figure() tset = prepare_dataset() for i in range(4): subplot1 = fig.add_subplot(2,4,i+1) subplot2 = fig.add_subplot(2,4,i+1+4) run_simulation(tset, 3, subplot1, subplot2) fig.show()
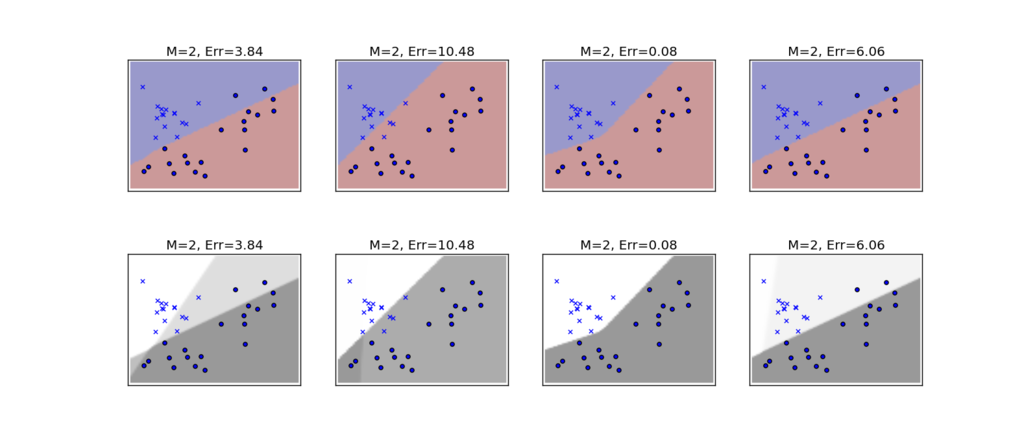
実行結果
Neural Networkは、極所解(極小点)が多いので、結果が初期値に大きく依存します。このコードでは、ランダムな4種類の初期値を使って、4種類の解を求めています。
上段は、 の境界線を示したもので、下段は、確率
の値を濃淡で示したものになります。
この中で一番良い結果を与えているのは、左から3番目の結果になります。
一方、一番左の例では、下段の濃淡を見ると、大きく4種類の確率の領域に分割されていることが分かります。これは、中間層のユニットが2個あることから理解できます。それぞれの中間層は、平面を直線で2つの領域に分類しており、それぞれの分類の組み合わせが出力層への入力になるので、結果として、4種類の組み合わせが出力層に入ります。