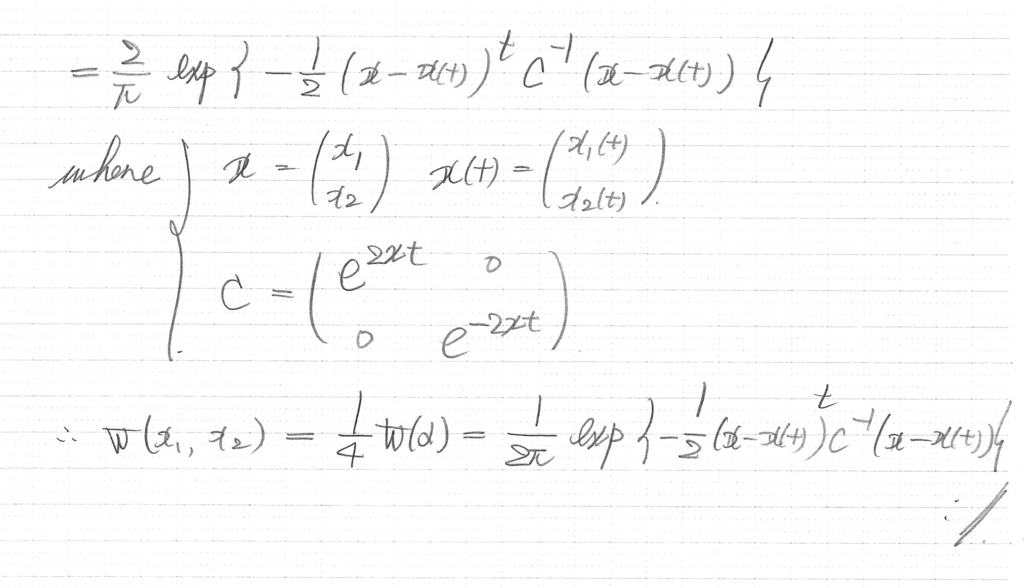Calculations on Coherent States and Squeezed States (4)

作者: D.F. Walls,Gerard J. Milburn
出版社/メーカー: Springer
発売日: 2010/02/12
メディア: ペーパーバック
この商品を含むブログを見る

This is intended to fill some gaps in calculation details in the book above.

5.1.1 Degenerate Parametric Amplifier

Preparation: basics of the interaction picture

Suppose that the Hamiltonian consists of the time-independent part $H_0$ plus the time-dependent interaction part $V(t)$ .

　 $H=H_0+V(t)$

Define the state vector and the interaction term in the interaction picture in conjunction with the ones in the Schroedinger picture

　 $\displaystyle{\mid\Psi_I(t)\rangle} := e^{\frac{i}{\hbar}H_0t}{\mid\Psi(t)\rangle}$

　 $\displaystyle V_I(t) := e^{\frac{i}{\hbar}H_0t}V(t)e^{-\frac{i}{\hbar}H_0t}$

You can prove that they follow the equation of motion below.

　 $\displaystyle \frac{d}{dt}{\mid\Psi_I(t)\rangle} = -\frac{i}{\hbar}V_I(t){\mid\Psi_I(t)\rangle}$

To calculate the expectation value for an operator $O$ , define the operator in the interaction picture and combine it with the state in the interaction picture.

　 $\displaystyle O_I(t) := e^{\frac{i}{\hbar}H_0t}Oe^{-\frac{i}{\hbar}H_0t}$

　 $\displaystyle \langle O(t)\rangle = {\langle\Psi_I(t)\mid}O_I(t){\mid\Psi_I(t)\rangle}$

Since the operator in the interaction picture is the same as the one in the Hisenberg picture with $H_0$ , it follows the equation of motion below.

　 $\displaystyle \frac{d}{dt}O_I(t) = \frac{i}{\hbar}[H_0, O_I(t)]$

In the special case, when the interaction operator $V_I(t)$ and your operators $O_I(t)$ in the interaction picture are time-independent, you have the following relationships.

　 $\displaystyle{\mid\Psi_I(t)\rangle} = e^{-\frac{i}{\hbar}V_It}{\mid\Psi(0)\rangle}$

　 $\displaystyle \langle O(t)\rangle = {\langle\Psi(0)\mid}e^{\frac{i}{\hbar}V_It}O_Ie^{-\frac{i}{\hbar}V_It}{\mid\Psi(0)\rangle}$ --- (4.1)

Especially, the latter means that the operator $O$ in the Heisenberg picture is obtained as

　 $\displaystyle O_H(t) = e^{\frac{i}{\hbar}V_It}O_Ie^{-\frac{i}{\hbar}V_It}$ --- (4.2)

Hence it follows the equations of motion below.

　 $\displaystyle \frac{d}{dt}O_H(t) = \frac{i}{\hbar}\left[V_I, O_H(t) \right]$ --- (4.3)

Degenerate Parametric Amplifier

　 $\displaystyle H_0=\hbar\omega a^\dagger a$

　 $\displaystyle V(t) = -\frac{i\hbar}{2}\chi(a^2e^{2i\omega t}-a^{\dagger 2}e^{-2i\omega t})$

Using the relationship (1.1), you can prove that:

　 $\displaystyle V_I(t) = -\frac{i\hbar}{2}\chi(a^2-a^{\dagger 2})$

So this is a special case of the time-independent $V_I$ .

Calculate $a,\,a^\dagger$ in the interaction picture.

　 $\displaystyle \frac{d}{dt}a_I(t) = \frac{i}{\hbar}[H_0,a_I(t)] = e^{\frac{i}{\hbar}H_0t} \frac{i}{\hbar}[H_0,a] e^{-\frac{i}{\hbar}H_0t} = -i\omega a_I(t)$

　 $\displaystyle \frac{d}{dt}a^\dagger_I(t) = \frac{i}{\hbar}[H_0,a^\dagger_I(t)] = e^{\frac{i}{\hbar}H_0t} \frac{i}{\hbar}[H_0,a^\dagger] e^{\frac{i}{\hbar}H_0t} = i\omega a^\dagger_I(t)$

Hence,

　 $a_I(t) = ae^{-i\omega t},\ a^\dagger_I(t) = a^\dagger e^{i\omega t}$

Now we define the rotated coordinates at a fixed time $t=t_0$ :

　 $Y_1+iY_2 = (X_1+iX_2)e^{i\omega t_0} = 2ae^{i\omega t_0}$

Convert it to the interaction picture and set $t=t_0$ .

　 $Y_{1I}(t_0)+iY_{2I}(t_0) = 2a_I(t_0)e^{i\omega t_0} = 2a = X_1+iX_2$

This means that the (time-independent) operators $X_1=a+a^\dagger$ and $X_2=-i(a-a^\dagger)$ represent the rotated coordinates at $t=t_0$ in the interaction picture.

Now you can use (4.2) and (4.3) to figure out the rotated coordinates in the Heisenberg picture to understand the physical effects on the initial state ${\mid\Psi_S(0)\rangle}$ .

　 $\displaystyle \frac{d}{dt}X_{1H}(t) = \frac{i}{\hbar}\left[V_I,X_{1H}(t)\right] = e^{\frac{i}{\hbar}V_It} \frac{i}{\hbar}\left[V_I,X_1\right]e^{-\frac{i}{\hbar}V_It}$

　　 $\displaystyle= e^{\frac{i}{\hbar}V_It}\frac{1}{2}\chi\left[a^2-a^{\dagger 2},a+a^\dagger\right]e^{-\frac{i}{\hbar}V_It}=e^{\frac{i}{\hbar}V_It} 2(a+a^\dagger) e^{-\frac{i}{\hbar}V_It}=\chi X_{1H}$

Likewise,

　 $\displaystyle \frac{d}{dt}X_{2H}(t) = -\chi X_{2H}$

Hence,

　 $\displaystyle X_{1H}(t) = e^{\chi t} X_1$

　 $\displaystyle X_{2H}(t) = e^{-\chi t} X_2$

So you can see the squeezing effect on the rotated coordinates.

Since $X_1,\,X_2$ are the rotated coordinates in the interaction picture, and they are time-independent, you can apply (4.1) to calculate the expectation value as