何の話かというと
上記の記事では、隠れUnitが2個という、世界で最もシンプルなニューラルネットワークを構成しました。
これをちょこっとだけ、拡張して遊んでみます。
隠れUnitを増やす
それぞれの隠れUnitは平面を直線で分割するわけですので、隠れUnitを増やせば分割線がどんどん増やせます。
前回のコードでは、下記の部分で隠れUnitの個数を指定していたので、これを変えてためしてみます。ここでは、4個にしてみます。
hidden1_units = 4
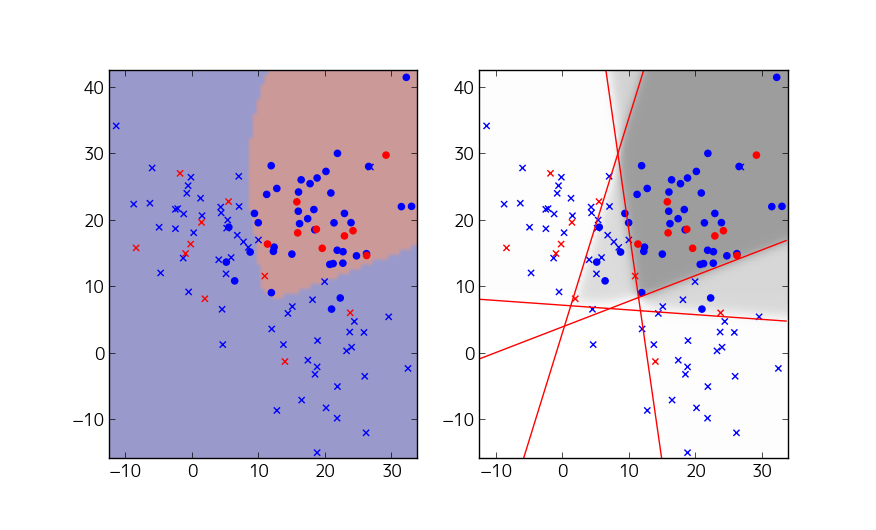
はい。予想通り、境界線がより複雑になりました。隠れUnitの数をどんどん増やすことで、どれほど複雑な関数でも表現できてしまいます。
ちなみに、上図の左側では、確率0.5を境界にして○と✕の領域を単純に分割していますが、右側を見ると、○と✕が混在した領域では、きちんと中間的な確率になっていることが分かります。
Activationを変えてみる
前回のコードでは、隠れUnitを次のように定義しました。
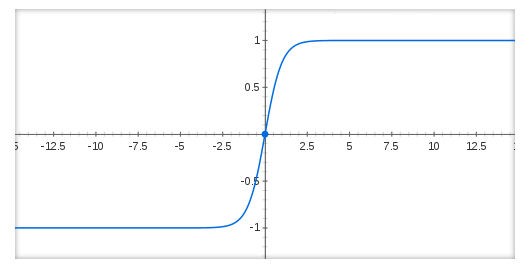
は、下図のように、原点付近で-1から1にひょこっと値が立ち上がる関数です。これがActivationです。
一方、Activationに使用する関数を取り替えることで、ニューラルネットワークの性能が変化することが知られています。ディープラーニングでよく使われるのが、次のReLU(ランプ関数)です。
コードの下記の部分を修正して、ReLUをActivationに使ってみます。
hidden1 = tf.nn.relu(tf.matmul(x, w0) + b0*mult)
# hidden1 = tf.nn.tanh(tf.matmul(x, w0) + b0*mult)
結果は、次のとおりです。
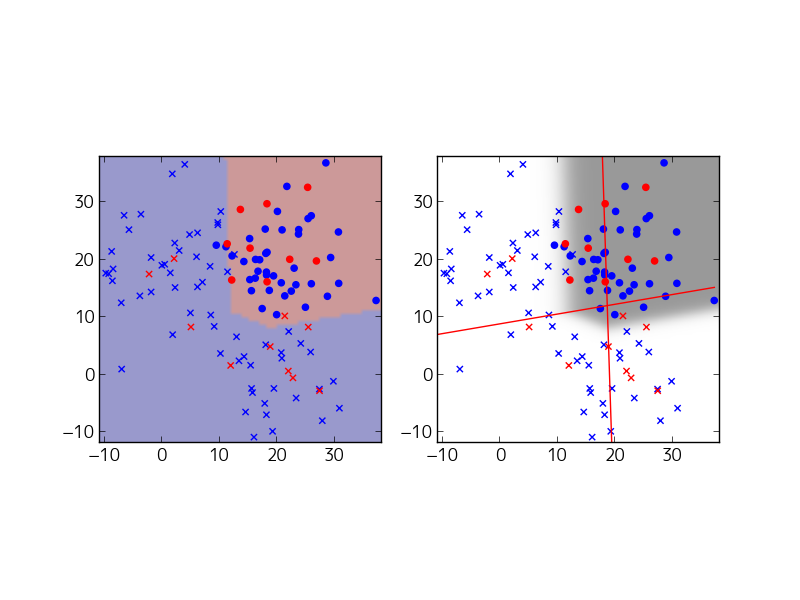
この例では、右上の領域がになっており、これが「◯の確率が高い領域」と判定されています。しかし、境界線をこえるとすぐに
の値が大きくなるわけではないので、境界線をはみだして確率が変化しています。結果として、単純な4分割よりもやや複雑な境界線を描くことに成功しています。
次回予告
今回は、1段の隠れ層に含まれるUnitの数を増やして、分割線を複雑にしていきました。しかしながら、結局は、直線の組み合わせで分割することしかできないという限界があります。次のステップは、隠れ層の後ろに、さらに隠れ層を追加して、隠れ層を2段にする拡張になります。これは、1段目の層で「特徴量(特徴変数)」を抽出して、それを元にして2段目の層で分類を行うという処理になります。いったいどういうことなんでしょうね・・・・?
次回の記事はこちらです。