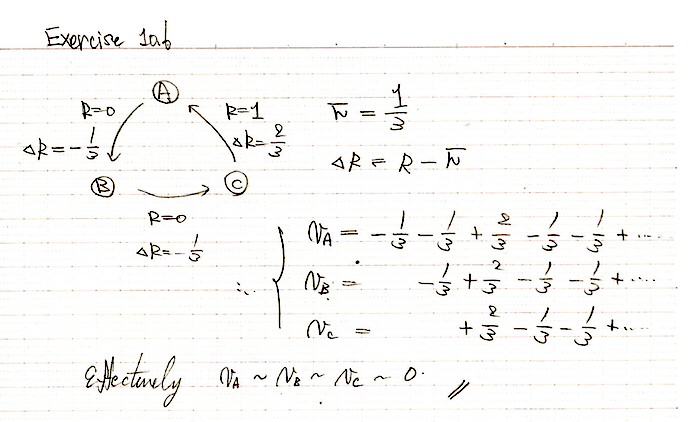Reinforcement Learning 2nd Edition: Exercise Solutions (Chapter 9 - Chapter 12)

Reinforcement Learning: An Introduction (Adaptive Computation and Machine Learning series)

作者:Sutton, Richard S.,Barto, Andrew G.
発売日: 2018/11/13
メディア: ハードカバー

Chapter 9

Exercise 9.1

Define a feature $\mathbf x$ as a one-hot representation of states $s_i$ , that is, $x_i(s_j) = \delta_{ij}$ .

Then, $v(s_i) = \mathbf w^{\rm T}\mathbf x = w_i$ .

Exercise 9.2

There are $n+1$ choices of $c_{ij}$ ( $c_{ij} = 0,\cdots,n$ ) for $j=1,\cdots,k$ .

Exercise 9.3

$n = 2,\ k=2$ . Hence there are $(1+n)^k=9$ features.

$c_{1.} = [0, 0]$
$c_{2.} = [1, 0]$
$c_{3.} = [0, 1]$
$c_{4.} = [1, 1]$
$c_{5.} = [2, 0]$
$c_{6.} = [0, 2]$
$c_{7.} = [1, 2]$
$c_{8.} = [2, 1]$
$c_{9.} = [2, 2]$

Exercise 9.4

Use rectangular tiles rather than square ones.

Chapter 10

Exercise 10.1

In this problem, sophisticated policies are required to reach the terminal state. Hence, an episode never end with an (arbitrarily chosen) initial policy.

Exercise 10.2

$\displaystyle {\mathbf w}_{t+1}={\mathbf w}_t + \alpha[R_{t+1}+\gamma\sum_a\pi(a\mid s_{t+1})\hat q(s_{t+1},a)-\hat q(s_t,a_t)] \nabla \hat q(s_t,a_t,\mathbf w_{t})$