PRML 第1章の「ベイズ推定によるパラメータフィッティング」の解説（その１）

ちょっと準備

正規分布の平均 $\mu$ と分散 $\sigma^2$ に関する計算をする際に、 $\beta = \frac{1}{\sigma^2}$ （つまり、 $\beta^{-1}=\sigma^2$ ）とおいて、 $\sigma^2$ の代わりに $\beta$ で計算することがあります。この方が計算が簡単になることが多いためですが、一般に、分散 $\sigma^2$ の逆数を精度（precision） $\beta$ と呼びます。精度が大きい（精度が高い）というのは、分散が小さくて確率分布が平均のまわりによく尖っていることになります。

これ以降の議論でも、言葉では「分散」と言いますが、数式上は精度 $\beta$ を用いて表します。

ベイズ推定による正規分布の決定

下記の記事では、ベイズ推定の一般的な考え方を紹介しました。ベイズ推定は、ある事柄の確率を観測データを元に洗練していく（「確信度」を高めていく）手法とも言えるでしょう。

Bayesの定理とBayes推定を初心者向けに説明してみる

一方、次の記事の後半にある「単純化した例で数値計算」では、未知の正規分布の「平均」と「分散」を観測データ（トレーニングセット）を元に「最尤推定」でフィッティングする方法を紹介しました。

PRML 第1章の「最尤推定によるパラメータフィッティング」の解説

しかしながら、記事の中で触れたように「最尤推定」以外の推定方法が存在しないわけではありません。ここでは、ベイズ推定のテクニックを用いてフィッティングしてみます。

ただし、少しだけ計算を簡単にするために分散は予め $\beta^{-1}$ （特定の定数）とわかっているとして、平均 $\mu$ が未知の正規分布について、観測データ（トレーニングセット）を元に「平均の値」をフィッティングします。

―― と言って、何をするのか想像できるでしょうか？　実は、ものすごい（ある意味適当な）ことをやります。

ベイズ推定は、『「観測データ」を元に「ある事柄の確率」を洗練していく』と説明しました。今の場合、「観測データ」に相当するのは「未知の正規分布から得られたトレーニングセット」です。一方、「ある事柄」に相当するのは・・・、そう、「平均 $\mu$ の値」です。つまり、ここでは、平均 $\mu$ がある値をとる確率 $P(\mu)$ が存在するとして、これをベイズの定理から計算していきます。

ここで言う確率は、「確信度」の意味で考えるとよいでしょう。つまり、 $\mu$ はいろいろな値の可能性があって、値ごとに「これが正しいかも？」という確信度 $P(\mu)$ が決まっていると思ってください。

それでは、何の前提条件（観測データ）も無い時、どのような確信（事前分布）を持つべきでしょうか？　特に根拠はないのですが、ここでは仮に $(\mu_0, \beta_0)$ を適当な定数として、

$P(\mu) = {\mathscr N}(\mu \mid \mu_0,\beta_0^{-1})$

と仮定します。これは、 $\mu = \mu_0$ の確率が最も高くなる正規分布です。

何の前提もあらへんのに $\mu_0$ の確率が高いってなんで分かるんや？

というツッコミは無視します。

―― というのは嘘で、 $\beta_0 \longrightarrow 0$ （分散が無限大）の極限をとると、これは、あらゆる $\mu$ について確率が一定のフラットな分布になります。ここでは、仮にこのような分布を想定しておいて、最後にこの極限でどうなるかを観察することにします。

ちなみに、前提条件が無い時の分布を「事前分布」と呼びますが、事前分布をどのようにとるかは、フィッティング条件を決める人が恣意的に選択することがよくあります。繰り返しになりますが、ここでやっているのは、「いろいろあるフィッティング条件の中の一例」を作っているにすぎません。そのような事前分布でフィッティングすれば、有用な結果（つまり、未知のデータをよりよく推定する関数）が得られるかは、試行錯誤を必要とする非常に難しい問題なのです。

それでは、未知の正規分布から、観測データ群（トレーニングセット） $\{x_n\}_{n=1}^N$ が得られたとします。このデータを前提条件とすると、先ほどの確率はどのように変化するでしょうか？　ベイズの定理を用いると次のように計算できます。

$P(\mu \mid {\mathbf x}) = \frac{P({\mathbf x} \mid \mu)}{\sum_{\mu} P({\mathbf x}, \mu)} P({\mu})$
（※分母の $\sum$ は本当は積分ですが、簡単のためにこのように記載しています。）

ここで、右辺分子の $P({\mathbf x} \mid \mu)$ は、未知の正規分布の平均が特定の値 $\mu$ を取る場合に、 $\{x_n\}_{n=1}^N$ が得られる確率ですので、次の通りです。

$P({\mathbf x} \mid \mu) = \prod_{n=1}^N{\mathscr N}(x_n \mid \mu,\beta^{-1}) = \left(\frac{\beta}{2\pi}\right)^{\frac{1}{2}}\exp\left\{-\frac{\beta}{2}\sum_{n=1}^N(x_n-\mu)^2\right\}$

また、分母の $\sum_{\mu} P({\mathbf x}, \mu)$ は、 $\mu$ には依存しない値ですので、最終的に、観測データ取得後の $\mu$ の確率（確信度）として次の関係式が成り立ちます。（ $\mu$ に依存する比例項だけを取り出しています。）

$P(\mu \mid {\mathbf x}) \propto P({\mathbf x} \mid \mu)P(\mu) \propto \exp\left\{-\frac{\beta}{2}\sum_{n=1}^N(x_n-\mu)^2-\frac{\beta_0}{2}(\mu-\mu_0)^2 \right\}$ ―― (1)

したがって、(1)の値を最大にする $\mu$ の値を見つければ、それが最も確率の高い（確信度が高い）値 $\mu = \mu_N$ ということになります。

なお、(1)をよく見ると $\exp$ の中は $\mu$ についての二次関数であり、(1)は $\mu$ についての正規分布になっていることが分かります。 $\mu$ について平方完成すると、次の結果が得られます。

$p(\mu \mid {\mathbf x}) = {\mathscr N}(\mu \mid \mu_N,\beta_N^{-1})$

ここに、

$\mu_N = \frac{\beta \mu_{\rm ML}+\frac{\beta_0}{N}\mu_0}{\beta+\frac{\beta_0}{N}}\,\,\,\,\left(\mu_{\rm ML} := \frac{1}{N}\sum_{n=1}^Nx_n\right)$

$\beta_N = \beta_0 + N\beta$

計算はこちら

この結果から重要な性質が読み取れます。

まず、最も確率の高い（確信度の高い）値 $\mu_N$ に着目すると、 $\beta_0 \longrightarrow 0$ の極限では、最尤推定と同じで、 $\mu_N = \mu_{\rm ML}$ となります。一方、 $\beta_0 > 0$ の場合、 $\mu_N$ とは、最尤推定よりも $\mu_0$ の方に寄った値になります。（ $\mu_N$ は、 $\mu_{\rm ML}$ と $\mu_0$ を $\beta : \frac{\beta_0}{N}$ の比に分割する値ですね。）

つまり、「 $\mu_0$ に近いほうが確率が高い」という事前分布（前提条件がない状態での確信度）に影響されて、前提条件をつけた後も $\mu_0$ に寄った答えとなるわけです。

ただし、十分な数の観測を行えば、事前分布の影響はなくなります。つまり、 $N \longrightarrow \infty$ の極限で $\mu_N = \mu_{\rm ML}$ となります。先ほど「事前分布のとり方は恣意的」と言いましたが、一般に十分な観測が行える環境下では、最終結果は事前分布に依存しないと期待することができます。大量のトレーニングセット（ビッグデータ？）があれば、前提が多少いい加減でも、それなりによい結果が得られると期待できるわけです。

ベイズ推定ならではの考え方

ここまでの結果を見ると「ベイズ推定も結局は最尤推定と同じじゃん」と言いたくなりますが、実は、重大な違いがあります。最尤推定で得られるのは、あくまでも、 $\mu$ に対する特定の推定値 $\mu_{\rm ML}$ だけです。一方、ベイズ推定の場合は、「最も確率（確信度）の高い値」としては最尤推定と同じですが（ $\beta_0 \longrightarrow 0$ 、もしくは、 $N \longrightarrow \infty$ の極限の場合）、それ以外の値についてもそれぞれの確率（確信度）が与えられました。

$p(\mu \mid {\mathbf x}) = {\mathscr N}(\mu \mid \mu_N,\beta_N^{-1})$ ―― (2)

つまり、ベイズ推定の立場では、最も確率の高い値だけを特別扱いするのではなく、あらゆる値について、その確率に応じた割合で、その可能性を認めるべきなのです。(2)は分散 $\beta_N^{-1}$ の正規分布ですので、 $\mu$ にはこの分散程度の不確定性が残っています。

$\beta_N^{-1} = \frac{1}{\beta_0 + N\beta}$

この式を見ると、 $N \longrightarrow \infty$ の極限では、分散は0になります。つまり、観測を行う前の $N=0$ の状態では、事前分布に従って $\beta_0^{-1}$ の不確定性がありますが、観測を積み重ねるに従って分散（不確定性）は減っていき、最終的には不確定性がなくなります。つまり、ベイズ推定の結論は、最尤推定と厳密に一致します。

しかしながら、 $N$ が有限の場合は、仮に $\beta_0 \longrightarrow 0$ の極限でも分散は残るので、この影響を無視するわけには行きません。

たとえば、あるトレーニングセット ${\mathbf x}$ が得られた場合、この「未知の正規分布」から次にある値 $x_0$ が観測される確率は、あらゆる $\mu$ における確率(2)の「期待値」として計算します。

$P(x_0 \mid {\mathbf x}) = \int P(\mu \mid {\mathbf x}) {\mathscr N}(x_0\mid\mu,\beta^{-1})\,d\mu$

　　　　　 $= \int {\mathscr N}(\mu \mid \mu_N,\beta_N^{-1}) {\mathscr N}(x_0\mid\mu,\beta^{-1})\,d\mu$

この積分は、次のように気合で実施することができます。

つまり、次の結果が得られました。

$P(x_0 \mid {\mathbf x}) = {\mathscr N}\left(x_0\,\middle|\,\mu_N,\beta^{-1}+\beta_N^{-1}\right)$

もともと未知の正規分布の分散は $\beta^{-1}$ と分かっていたにも関わらず、次の $x_0$ はそれよりも $\beta_N^{-1}$ だけ大きな分散で推定しています。これは、観測データが少ないために、 $\mu_N$ が真の平均 $\mu$ と同じである自信がない事に対応します。 $\mu_N$ に含まれる誤差（分散 $\beta_N^{-1}$ ）を考慮して、その分だけ大きな分散で次の $x_0$ を予測しているというわけです。

実際、観測データを増やしていくと（つまり、 $N$ を大きくしていくと）、 $\beta_N$ が大きくなっていくので、 $N \longrightarrow \infty$ の極限では、

$P(x_0 \mid {\mathbf x}) = {\mathscr N}\left(x_0\,\middle|\,\mu_N,\beta^{-1}\right)$

となります。つまり、 $\mu_N$ が真の平均 $\mu$ と同じであると自信を持って言えるので、もともとわかっている分散 $\beta^{-1}$ で予測ができるわけです。

数値計算で確認

実際に数値計算した結果をグラフにして見てみます。

これから推定する「未知の正規分布」として、平均2, 分散1の正規分布を用意して、ここから100個のサンプルを取り出します。100個のサンプルから先頭の 2, 4, 10, 100個をトレーニングセットとして用いて、平均 $\mu$ に対するBayes推定を行います。平均 $\mu$ の事前分布は、平均-2, 分散1とします。

まず、次式で表される「 $\mu$ の事後分布」をグラフにするコードです。

$p(\mu \mid {\mathbf x}) = {\mathscr N}(\mu \mid \mu_N,\beta_N^{-1})$

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame

from numpy.random import normal
from scipy.stats import norm

if __name__ == '__main__':

    mu_true = 2.0
    beta_true = 1.0

    mu_0 = -2.0
    beta_0 = 1.0

    fig = plt.figure()
    ax = {}
    ds = normal(loc=mu_true, scale=1.0/beta_true, size=100)

    for c, n in enumerate([2,4,10,100]):
        trainset = ds[0:n]
        mu_ML = np.mean(trainset)
        mu_N = (beta_true*mu_ML + beta_0*mu_0/n)/(beta_true+beta_0/n)
        beta_N = beta_0 + n*beta_true

        # Show fitting curves
        ax[c] = fig.add_subplot(2,2,c+1)
        ax[c].set_title("Datapoints=%d" % n)
        linex = np.arange(-10,10.1,0.1)

        # distribution of estimated mu
        sigma = 1.0/beta_N
        mu_est = norm(loc=mu_N, scale=np.sqrt(sigma))
        label = "mu_N=%.2f\nvar=%.2f" % (mu_N, sigma)
        ax[c].plot(linex, mu_est.pdf(linex), color='red', label=label)
        ax[c].legend(loc=2)

        # data points of the training set
        ax[c].scatter(trainset, [0.2]*n, marker='o', color='blue')
        ax[c].set_xlim(-5,5)
        ax[c].set_ylim(0)
    fig.show()

実行結果は次のようになります。

このグラフは、元の正規分布を示しているのではなく、平均 $\mu$ の確率を示している点に注意してください。使用するデータを増やすにつれて、グラフの中心 $\mu = \mu_N$ が、事前分布の中心 $\mu = -2$ から、正しい平均 $\mu = 2$ に変化していることが分かります。また、その中心の値が正しいという「確信度」が上がって、グラフの広がり（分散）が狭まっていきます。

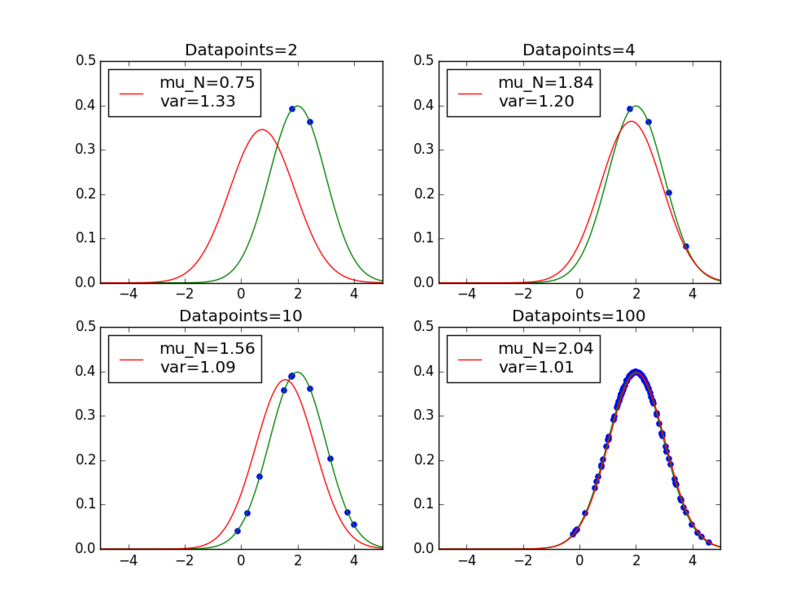
続いて、次に取得されるデータの推定を示す下記のグラフを描きます。これは、「未知の正規分布」に一致するべきものになります。

$P(x_0 \mid {\mathbf x}) = {\mathscr N}\left(x_0\,\middle|\,\mu_N,\frac{1}{\beta}+\frac{1}{\beta_N}\right)$

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame

from numpy.random import normal
from scipy.stats import norm

if __name__ == '__main__':

    mu_true = 2.0
    beta_true = 1.0
    mu_0 = -2.0
    beta_0 = 1.0

    fig = plt.figure()
    ax = {}
    ds = normal(loc=mu_true, scale=1.0/beta_true, size=1000)

    for c, n in enumerate([2,4,10,100]):
        trainset = ds[0:n]
        mu_ML = np.mean(trainset)
        mu_N = (beta_true*mu_ML + beta_0*mu_0/n)/(beta_true+beta_0/n)
        beta_N = beta_0 + n*beta_true

        ax[c] = fig.add_subplot(2,2,c+1)
        ax[c].set_title("Datapoints=%d" % n)
        linex = np.arange(-10,10.1,0.1)

        # Correct distribution
        orig = norm(loc=mu_true, scale=np.sqrt(1.0/beta_true))
        ax[c].plot(linex, orig.pdf(linex), color='green')

        # Estimated distribution
        sigma = 1.0/beta_true+1.0/beta_N
        mu_est = norm(loc=mu_N, scale=np.sqrt(sigma))
        label = "mu_N=%.2f\nvar=%.2f" % (mu_N, sigma)
        ax[c].plot(linex, mu_est.pdf(linex), color='red', label=label)
        ax[c].legend(loc=2)

        # Datapoints of the training set
        ax[c].scatter(trainset, orig.pdf(trainset), marker='o', color='blue')
        ax[c].set_xlim(-5,5)
        ax[c].set_ylim(0)
    fig.show()