「Characterizing Quantum Supremacy in Near-Term Devices」を読み解いてみた

これは何かというと

自分の勉強のために、Characterizing Quantum Supremacy in Near-Term Devices を読み解いたメモです。（若干、ポエムも混じってます。すいません。。。）

Quantum Supremacy とは？

（参考資料）
・Quantum computing and the entanglement frontier

我々の物質世界（特にミクロな世界）は量子力学の原理によって動いていますが、これまで人類は、「量子的な現象を人為的に自由にコントロールする」ということはできていませんでした。つまり、既知の現象を量子力学で説明することはできても、「量子力学の原理を用いることで何が可能で何が可能でないのか」という根本的な問はまだ突き詰められていませんでした。量子力学の原理で動作する量子計算機が実現できれば、これまでに知られていなかった量子力学の可能性を探求する道が開けるとの期待があります。やや大げさに言うと、「マクロな世界で量子的現象を活用する」という人類の夢が実現するかも知れません。

しかしながら、ミクロな世界でのみ現れる量子的な現象をマクロな計算機として実装することが本当に可能かどうか、という根源的な疑問もあります。さらに、小さな規模であれば、量子計算機の処理を古典コンピューター（スパコン）でシミュレーションする技術はすでに確立されており、仮に量子計算機が実装できたとしても、古典コンピューターでシミュレーションできる規模の計算しかできなければ、量子計算機の真の優位性はありません。したがって、「古典コンピューターではシミュレーションできない規模の量子計算を実物の量子計算機で実行してみせる」という事は、量子計算機の研究・開発における１つの夢の到達点と考えられてきました。

このような処理を実現することができれば、量子計算機の真の優位性、つまり、「Quantum Supremacy」が実証できるというわけです。

ちなみに、古典コンピューターで量子計算機をシミュレーションする際の主な制約は、計算に必要なメモリ量になります。計算に必要なメモリ量は qbit 数に対して指数的に増えるという特性があり、50qbit 程度で 1PB 以上のメモリが必要となります。

Quantum Supremacy を実証するために必要なこと

「古典コンピューターではシミュレーションできない規模の量子計算を実物の量子計算機で実行してみせる」というのは、概念的にはわかりやすい目標ですが、実際にこれを実証するには、いくつかのステップが必要です。

・「古典コンピューターではシミュレーションできない量子計算処理」を考え出す。（実際に古典コンピューターではシミュレーションが困難であることを証明する必要もあります。）

・その処理を量子計算機で実行する。

・実行結果が正しいことを証明する。

「古典コンピューターではシミュレーションできない量子計算処理」はいろいろ考えられますが、「あと500年ぐらいはまだ技術的に無理・・・」と思われるような処理を考えていては話が先に進みません。本論文では、現在の量子計算機の技術を鑑みて、「Near-Term Devices」、すなわち、あと数年以内に実装できそうな範囲での「古典コンピューターではシミュレーションできない量子計算処理」の例を提唱して、さらにその実行結果が正しいことを実証する手法について解説をしています。

本論文が提唱する量子計算処理

本論文では、上述の処理として Quantum Random Circuit を取り上げています。Random Circuit と言っても本当にデタラメに動作するわけではありません。量子ビットに対して、とても複雑な処理を繰り返すことで、量子ビットの初期状態に依存しない「一見するとランダムな重ね合わせ状態」を実現するという量子回路になります。

ここで注意が必要なのは、「一見するとランダムな状態」ではなくて、「一見するとランダムな重ね合わせ状態」という点です。量子計算機では、複数の状態を同時に持った「重ね合わせ状態」を利用する、という話を聞いたことがあると思いますが、ここでは、n 個ある量子ビットのあらゆる組み合わせをランダムな重みで重ね合わせた状態を実現します。たとえば、4個の量子ビットがあった場合、その状態は、

・0000, 0001, 0010, 0011, ・・・, 1111

の 2^4 通りありますが、こららすべての状態がランダムな重みで重ね合わせられた状態だと思ってください。

この時、この4つの量子ビットの状態をまとめて読み出すと、ある確率で、どれか1つの組み合わせ（0000 とか 0010 とか 1101 とか）が得られます。この確率は、それぞれの状態の重み（の2乗）によって決まります。この際、それぞれの確率がランダムであり、決して同じ確率が集中することはない、という点が１つのポイントです。

ーーなぜでしょう？

たとえば、この量子計算機がぶっ壊れている場合を考えます。実際に何が起きるかはぶっ壊れ方に依存しますが、量子計算機の実装上の困難の1つが「量子ビット間の相関を維持する（かっこよく言うと、Entanglement を保持する）」という点にあります。Entanglement がうまく保持できなかった場合、各量子ビットは独立に振る舞うため、それぞれの観測される値は独立に決まってしまいます。たとえば、各量子ビットは、それぞれ 1/2 の確率で独立に「0」か「1」の値をとるようなことになります。この場合、「0000」も「0010」も「1101」すべて出現確率は同じになります。より一般的に、確率 p / 1-p で「0」か「1」の値をとるようになった場合でも、「0001」と「0010」と「0100」と「1000」はすべて出現確率が同じになることがわかります。

言い換えると、4つの量子ビットのあらゆる組み合わせに対して、それぞれに微妙に異なる出現確率を与えるというのは、量子ビットの間に相関関係（すなわち、Entanglement）があってはじめて実現できることであり、このような Quantum Random Circuit は、量子計算機の信頼性を測る上ではよいベンチマークになると考えられます。

Porter-Thomas 分布について

前述の「ランダムな重ね合わせ状態」をもう少し正確に説明します。n 個の量子ビットがある場合、古典的には $N=2^n$ 個の状態が存在します。これらの重ね合わせ状態というのは、2^n 個の古典状態を基底とする 2^n 次元の複素ベクトルとして表されます。量子力学っぽく書くとこんな感じです。

　 ${\mid\psi\rangle} = c_0{\mid 00..000 \rangle} + c_1{\mid 00..001 \rangle}+ c_2{\mid 00..010 \rangle}+ c_{N}{\mid 11..111 \rangle}$

各係数 $c_i$ は複素数で、 $|c_i|^2$ が i 番目の状態が観測される確率になります。全確率が 1 になるために、これらには、

　 $\displaystyle \sum_{i=0}^N |c_i|^2 = 1$

という束縛条件がついています。直感的に言うと N 次元（複素）空間上の球面上の1点になります。この球面上の1点をランダムに選んで上記の状態 ${\mid\psi\rangle}$ を決定した際に得られるのが、前述の「ランダムな重ね合わせ状態」に対応します。量子計算機で実装する Random Circuit の場合は、ランダムに点を選ぶわけではなく、決定論的にある1つの点に到達しますが、その点が何か特定の基底状態に近づいたりすることなく、あたかもランダムに選んだかのような点に対応することになります。

それでは、このようにして選ばれた状態 ${\mid\psi\rangle}$ の場合、各基底状態が観測される確率、すなわち、 $|c_i|^2$ の値はどのように散らばるのでしょうか？　Jupyter Notebook を使って、N 次元（複素）空間上の球面上の1点をランダムに選んでみると次のような結果が得られます。

これは、 $n=20$ の場合の例で、 $N=2^{20}=1048576$ 個の基底状態を確率 $|c_i|^2$ の昇順にソートした上で、それぞれの確率をグラフにしたものです。確率の値が滑らかに単調増加しており、さまざまな確率が混在していることがわかります。論文の中では、次のグラフが掲載されており、ちょうどこれと同じものになります。

なお、上図の赤いラインは、量子回路上でエラーが発生したと仮定した場合の結果です。この場合は、Entanglement がなくなって、すべての状態がほとんど同じ確率の一様分布になっていることがわかります。

また、こららのグラフは、生の確率の値を示したものですが、この量子状態を実際に観測して状態のサンプリングを行った場合に、「生の確率が p」の状態が実際に観測される確率「 ${\rm Pr}(p)$ 」を計算することができます。

・・・確率の確率って、お前は何を言ってるんだ。。。

とは言わないで下さいね。。。。

たとえば、今の例の場合、一番右端の状態はむっちゃ確率が高いのですが、これは状態としては1つしかありません。一方、真ん中あたりの状態は、同じような確率をもった状態が比較的たくさんあります。したがって、実際に観測した場合は（状態数の多さに助けられて）このあたりの確率をもった状態がより多く（つまり、より高い確率で）観測されることになります。

（参考）
・Asymptotic equipartition property を説明するコードサンプル

で、これもまた、Jupyter Notebook をつかって、実際にサンプリングした結果をヒストグラムに示すと次のようになります。

これは、縦横でスケールを調整しており、横軸は $Np$ 、縦軸は $\log_e {\rm Pr}(Np)$ になっています。ほぼ直線的な変化をしていることがわかります。

そして、論文に掲載されている、これと同じ図がこちらになります。

青色のグラフが量子回路上にエラーがない理想的な状態で、エラーが増えると垂直に立ち上がっていくことがわかります。前述のようにエラーが発生すると、みんな同じ確率になってしまうためです。極端な例で、完全な一様分布になった場合、すべての状態は p=1/N の確率ですので、 $Np = 1$ の部分に一本だけ棒が立つことになります。

ちなみに、エラーがない理想的な場合のこの分布は、Porter-Thomas 分布と呼ばれており、量子カオス理論の中で登場するものになります。前述の Random Circuit の場合、この量子回路で量子ビットを変換していくと、対応する量子状態 ${\mid\psi\rangle}$ は $N=2^n$ 次元の球面上を複雑な軌跡で乱雑に移動することになり、ちょうど、量子カオス系の一種とみなすことができるというわけです。

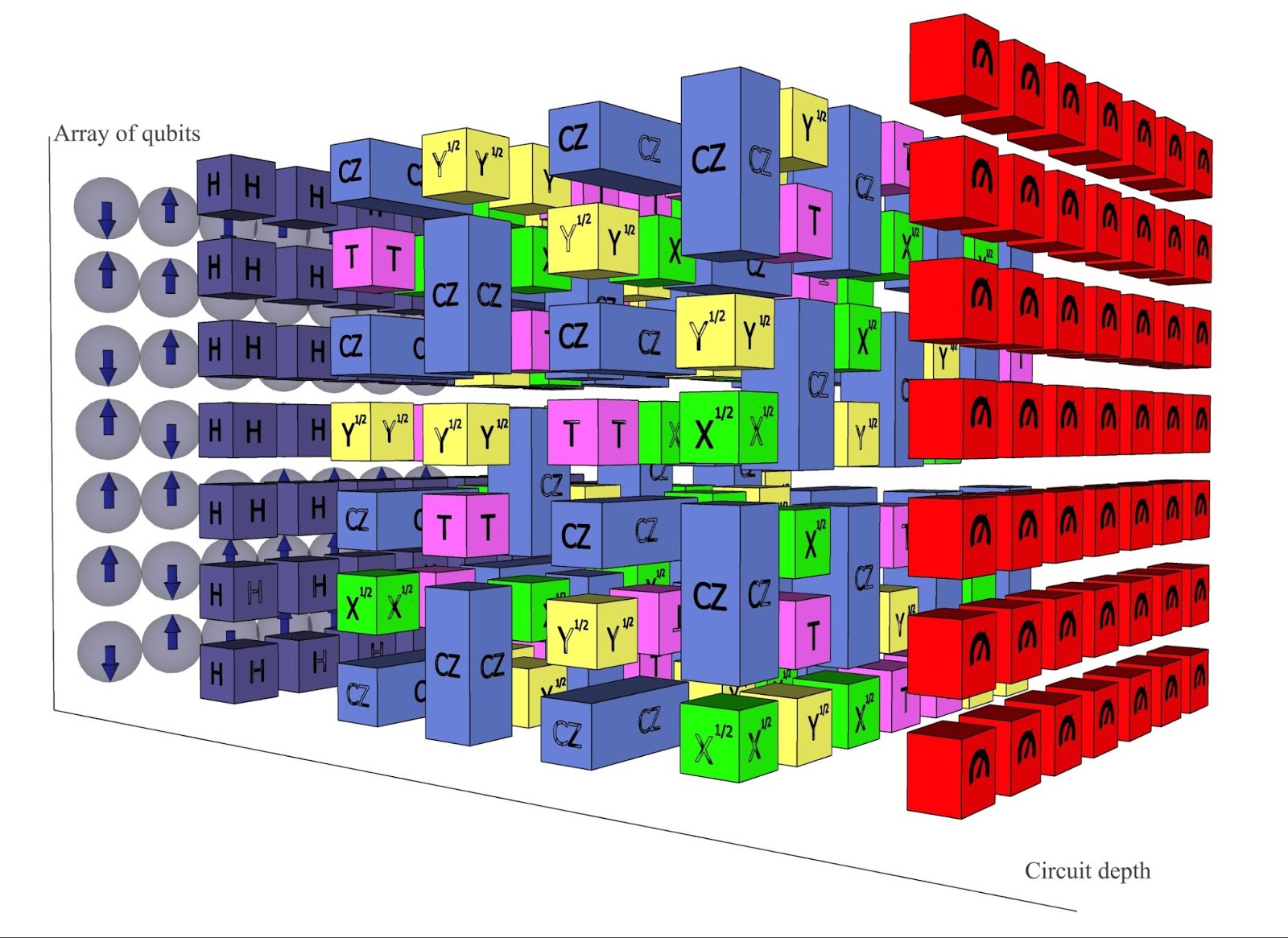
ちなみに、ここまで、Random Circuit の実体を説明してきませんでしたが、絵にするとこんな感じの量子回路です。

特徴としては、平面上に配置された量子ビットに対して、隣り合う量子ビット間での演算のみがほどこされています。現在の技術では、遠く離れた位置の量子ビット間での演算を実装することがまだ困難なのですが、これであれば、現在の技術で十分に実装できる可能性があるというわけです。量子ビット数としては、 $7\times 7=49$ qbit を実現すれば、現在のスパコンでの計算能力を超える（スパコンではシミュレーションすることができない）との推測が論文内ではなされています。

Porter-Thomas 分布の確認方法

さあこれで、Near-Term devices で Quantum Supremacy が実証できる（かもしれない）量子回路が決まったわけですが、次の課題は、これを実装して動作させた際に、本当に正しく（エラーを混入させずに）動作していることをどうやって検証するかです。理屈の上では、量子回路を通した後の量子ビットを観測して、その分布が前述の Porter-Thomas 分布に従っていることを確認すればよいわけですが、これはそれほど簡単ではありません。

まず、量子ビットの状態は一度観測するとぶっ壊れてしまうので、多数の状態をサンプリングするには、同じ回路を何度も繰り返し動作させて、観測を繰り返す必要があります。この時、前述のようなヒストグラムをきれいに描くためには、相当な数をサンプリングする必要があります。たとえば、 $n=20$ qbit の場合を考えると、観測される状態数は全部で $N=2^{20}=1048576$ 通りあります。しかも、それぞれの観測確率は先のグラフのようになだらかに変化しているので、特定の状態が集中して観測されることはあまりなさそうです。仮に 100 回観測したとしても、それらは、すべて別々の状態である可能性が高いです。つまり、この程度のサンプル数では、Porter-Thomas 分布と（量子回路上でエラーが発生している際の）一様分布を区別することができないのです。

そこで、より効率的にこれらを区別するために、この論文では、次の量（cross entropy difference）を計算することを提案しています。

　 $\displaystyle \Delta H(p_A) = H_0 - H(p_A,p_U) = \sum_{j} \left( \frac{1}{N}-p_A(x_j \mid U) \right)\log\frac{1}{p_U(x_j)}$

この量は、Random Circuit の種類 $U$ に依存するものですが、さまざまな Random Circuit を取り混ぜて実験した際の平均値

　 $\displaystyle\alpha = E_U\left[\Delta H(p_{\exp})\right]$

を考えると、この値は、中心極限定理により、実際の観測サンプル $\{x_j^{\exp}\}_{j=1}^m$ を用いた次の値で近似されます。

　 $\displaystyle \alpha \simeq H_0 - \frac{1}{m}\sum_{j=1}^m\log\frac{1}{p_U(x_j^{\exp})}$ --- (1)

（このあたりの計算の詳細は論文を参照してください。。。。）

この値は、 $1\ge \alpha\ge 0$ の範囲を取り、サンプルの分布が Porter-Thomas 分布であれば 1 になり、一様分布であれば 0 になります。つまり、この値が 1 に十分近ければ、量子回路にはエラーが混入していないと確認することができるのです。

実際の実験手続き

さて・・・。これで無事に Quantum Supremacy が実証できるような気がしてきましたが、実は前述の手法には問題が残っています。

それは、(1) に含まれる $p_U(x_j^{\exp})$ という値です。これは、「量子回路 U を用いた際に状態 $x_j^{\exp}$ が観測される確率」を表わすものですが、これってどうやって計算するのでしょうか？　もちろん、量子回路 U の内容が決まれば理論的には計算可能ですが、いま挑戦しようとしているのは、スパコンでもシミュレーションできないような量子回路です。この値を計算するには、量子計算機の能力が必要で、そんな量子計算機の存在を証明しようとしている時に、そんな量子計算機で計算できるわけが、ぐぁぁぁぁぁぁ。

というわけです。

この論文では、この「鶏-卵」問題の回避策として、次のような手法を提案しています。

まずはじめに、古典コンピューターでシミュレーションできる規模の量子ビット数で実験を行います。つまり、Random Circuit U をランダムに1つ用意して、観測サンプル $x_j^{\exp}$ を取得して、それに対して $p_U(x_j^{\exp})$ を古典コンピューターで計算します。この手続を何度も繰り返すと (1) の式によって $\alpha$ の値が計算されます。

そして、量子ビット数を徐々に増やしながら、それぞれで $\alpha$ を求めると、おそらくは、量子ビット数が増えるに従って計算精度が下がって $\alpha$ は 1 から徐々に減っていくと想像されます。そして、古典コンピューターで計算できるぎりぎりの所まで量子計算機が一定の精度で動くことが確認できれば、最後に、いよいよ、古典コンピューターが使えないサイズでの実験を行います。この場合の $\alpha$ は直接には計算できませんが、それ以前の実験結果に基いて、何らかの理屈で外挿できるだろう、というのが論文の主張になります。

ただし・・・・、実際にどういう理屈で信頼のおける外挿が可能になるのかは、私には論文からは読み取れませんでした。。。。もしかしたらここの詳細は、まだこれからの課題なのかも知れません。その代わりかどうかはわかりませんが、論文の中では、スパコンによるシミュレーションを用いて、 $\alpha$ の値がどのように変化するかを予想したグラフが紹介されています。

これは、エラーの発生率ごとに、量子ビットが増えると $\alpha$ がどのように変化するかを示したもので、エラーが無い理想的な状態では、常に $\alpha=1$ が保たれています。エラーがある場合、量子ビットが増えるにしたがって、エラーの発生率がより大きく影響することが読み取れます。論文の中では、現在の最新技術を用いれば、49 qbit において、 $\alpha=0.1$ が達成できるだろうとの予測がなされています。