フーリエ級数のアニメーションを作成するJupyter Notebook

あらゆる関数を三角関数の重ね合わせで表現する仕組みです。たとえば、次のような三角関数の足し合わせを考えます。

　 $f(x)=c+\sum_{n=1}^\infty \left\{a_n\cos(nx)+b_n\sin(nx)\right\}$

この時、係数 $c, a_n, b_n$ をうまいこと調整すると、 $-\pi \le x \le \pi$ の範囲で定義された任意の連続関数 $f(x)$ が表現できてしいます。係数の計算方法は次の通りです。

　 $c=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\,dx$

　 $a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)\,dx$

　 $b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)\,dx$

・・・という方のために、これを動画で再現するコードを用意しました。

※実行環境の準備は下記の「GCEのVMインスタンスを利用する場合」というセクションを参照してください。

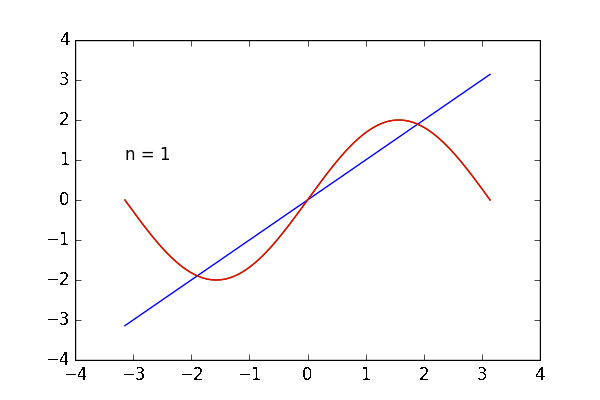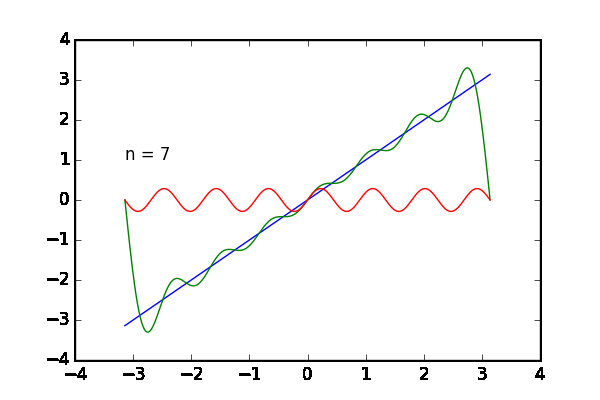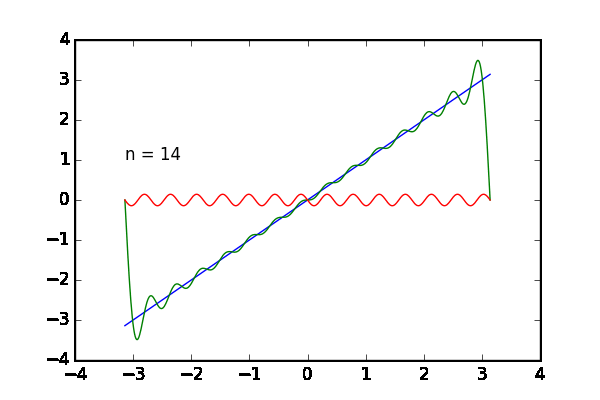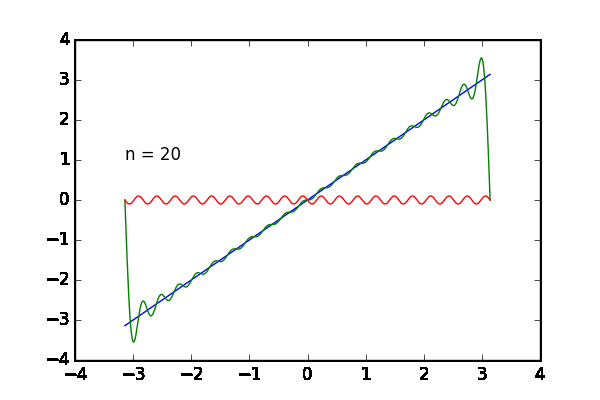
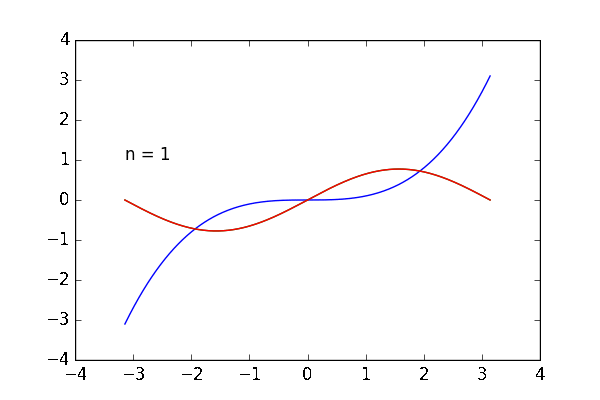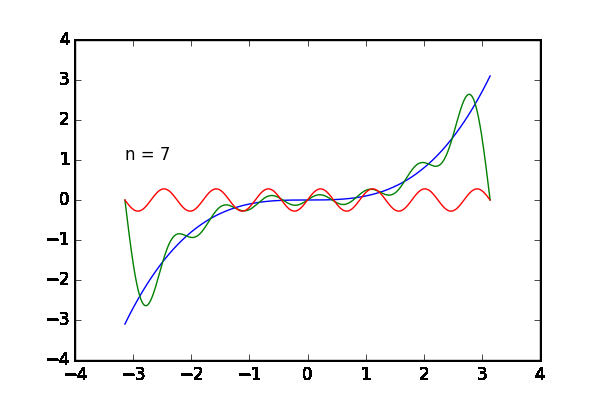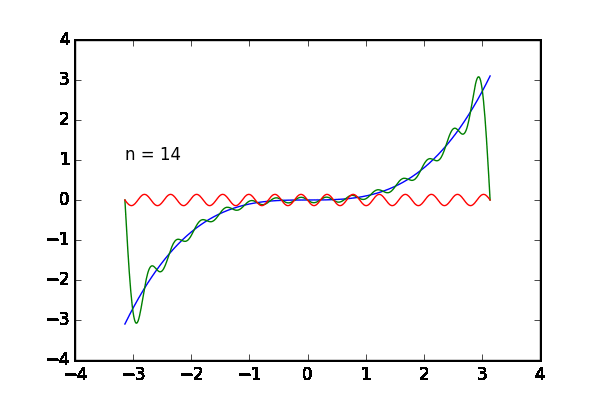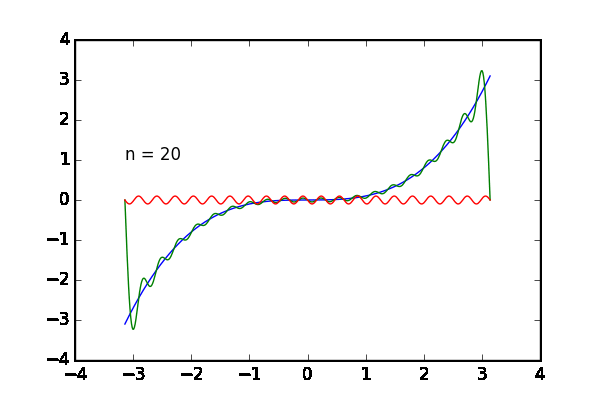
完成した動画は次の通りです。足し合わせる波の数 $n$ を増やすと目的の関数 $f(x)$ に近づいていく様子が観察できます。青のグラフが目的の関数 $f(x)$ 、緑のグラフが $n$ 個まで足した状態、赤いグラフは最後に足した $n$ 番目の波です。

Disclaimer: All code snippets are released under Apache 2.0 License. This is not an official Google product.

めもめも