Ising Modelとは？
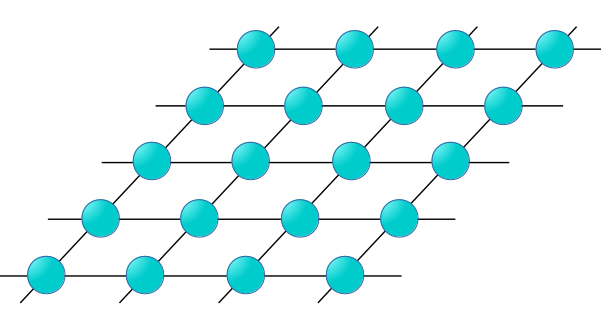
Ising Model（イジングモデル）とは、結晶を構成する原子の「スピン」の向きを計算する簡易的なモデルです。下図のように２次元の平面上に原子が整然と並んだ、架空の「結晶」を考えます。（本物の結晶は３次元にならんでいますが、話を簡単にするために２次元にさせてください。）
図の上では、それぞれの原子はピタッっと静止していますが、みなさんご存知のように、実際の原子はその場でプルプル震えています。温度が高いと激しくプルプルしていて、温度が下がるとプルプルはおさまっていき、絶対零度（−273.15 ℃）になると完全に静止します。（ちなみに、高温の金属をさわると「あちっ！」となりますが、これは、微視的には、激しくプルプルする原子が手の表面の神経を刺激するためにおきると考えられます。）
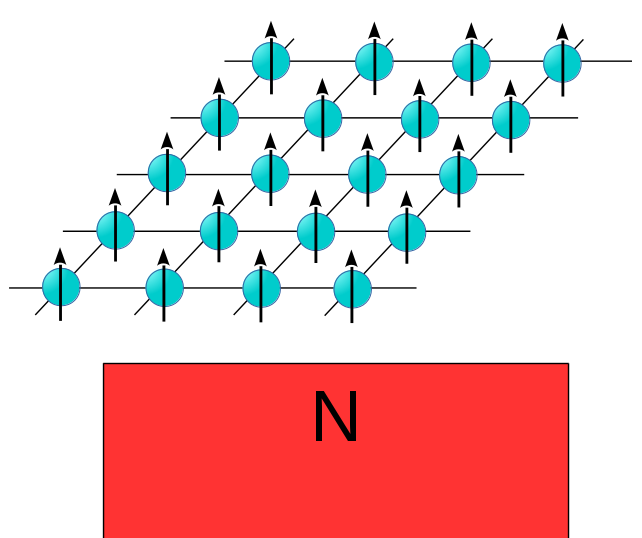
ここでさらに、それぞれの原子は「スピン」を持っているものとします。スピンと言っても原子が回転しているわけではなくて、原子の中に微小な「棒磁石」が埋め込まれていると思ってください。一般には、この棒磁石はいろんな方向を向く可能性がありますが、話を簡単にするために、「上向き（N極が上にくる）」か「下向き（N極が下にくる）」のどちらかだけをとるものとします。
この結晶の下から巨大な磁石のN極を近づけると、原子のスピンがピシッと上向きにそろう様子が想像できると思います。
それでは、このような外部の磁石がない場合、原子のスピンはどのように振る舞うでしょうか？ 高温の状態では、原子のプルプルにつられて、スピンもランダムに上向いたり、下向いたりを繰り返します。ただし、ここで、
「隣り合った原子のスピンは、できるだけ同じ向きを向きたがる」
という想定を置きます。これは実際には、スピン間の相互作用を量子力学的に計算して分かることなのですが、ここでは、そういうもんだとしておきます。
物理学では、このような「変化の方向」を記述するのに「エネルギー」の概念を利用します。エネルギーにもいろんな種類がありますが、ここでは「ポテンシャルエネルギー」の事になります。高い位置にある物体は、支えがなければ勝手に下に落ちてきますが、これは、「高いところの方が低いところよりも（ポテンシャル）エネルギーが高いから」というように考えます。つまり、物体は、エネルギーの低い状態に向かって変化していきます。
（ここでは熱力学の問題を考えているので、正確には「自由エネルギー」なんですが。。。ゴニョゴニョ。）
そして、「隣り合った原子のスピンの向きがそろいたがる」という現象は、隣り合った原子（原子１，原子２とします）の間のエネルギーを次のように定義することで表現できます。
E = -J * S1 * S2
J：正の定数
S1：原子１のスピンの向き（上＝１，下＝−１）
S2：原子２のスピンの向き（上＝１，下＝−１）
つまり、スピンの向きが揃っていると E = -J で、スピンの向きが反対の場合は E = +J ということです。スピンの向きが揃っている方がエネルギーが低いというわけです。
ある１つの原子に着目すると、まわりに４つの原子があるので、エネルギーの最小値は E = -4J （５個の原子がすべて同じ向きの場合）になります。
温度による状態の変化
それでは、このような性質の結晶を高温状態から、徐々に温度を下げるとどうなるか考えてみましょう。高温の状態では、原子のプルプルが激しいため、隣り合った原子の影響など無視して、それぞれの原子のスピンはでたらめに上を向いたり、下を向いたりしています。しかしながら、温度が下がってくると、隣の原子の影響が無視できなくなりだんだんと同じ方向にそろいはじめます。（上向きにそろうのか、下向きにそろうのか、という哲学的な問題はありますが・・・・。）絶対零度で原子が静止すると、最終的には、全部が上向き、もしくは、全部が下向きの状態で安定化すると予想されます。
では、この予想をもう少し数学的に表現してみましょう。統計熱力学をつかってゴニョゴニョと計算すると、次のような数式が得られます。（本当は、ボルツマン定数とかあるんですが、そこは目をつむって・・・。）
これは、ある原子の周りにある４つの原子のスピンを {S1,S2,S3,S4} とした時に、真ん中にある原子のスピンが上を向く確率を計算する式になります。たとえば、まわりのスピンがすべて上向きだとすると、温度を横軸として、次のようなグラフになります。
温度が高い場合は、上を向く確率はほぼ0.5(=1/2)です。つまり、原子のプルプルが激しくて上を向くか下を向くかは半々の確率です。しかしながら温度が下がると、上を向く確率が上がっていき、絶対零度では、確率１で上を向くことが分かります。ここで、Tは絶対温度（全体零度がT=0）を表します。
ただしこれは、ある原子に注目して、その周りの原子のスピンが固定されている前提で、その原子がどちらを向くかを計算しているだけです。実際には、周りの原子たちもさらにその周りに原子に影響されて上を向いたり下を向いたりしています。これら多数の原子の動きをまとめて計算する方法はないのでしょうか？
Gibbsサンプリング
ここで登場するのが「Gibbsサンプリング」というシュミレーションの技法です。このシュミレーションでは、最初、多数の原子のスピンの向きをランダムに決めておきます。
この状態で任意の1つの原子をランダムに選択して、周りの原子のスピンの向きを見て、先ほどの確率の公式に従って、スピンの向きを決定します。具体的には、0〜1の浮動小数点の乱数を発生して、Pより小さければ、スピンの向きを上にして、Pより大きければスピンの向きを下にします。つぎに、また別の原子をランダムに選択して同じことをします。これを順番に繰り返して、結晶に含まれるすべての原子についてこの操作を行います。さらにこの状態を出発点として、先ほどと同じ操作（すべての原子について、ランダムな順番で向きを決定していく）を行います。これを何度も繰り返すことで、現実の原子のスピンの動きをシュミレーションしようというわけです。現実の原子は、すべてが同時に動いている「パラレル処理」の世界ですが、これをランダムな順番の「シーケンシャル処理」に置き換えているわけです。
もちろん、この方法が現実のパラレル処理をどこまで正確に再現するかは議論する必要がありますが、まずは、実際にシュミレーションを行って、「もっともらしい」結果が得られるか見てみましょう。
・・・・・結果が出ました。
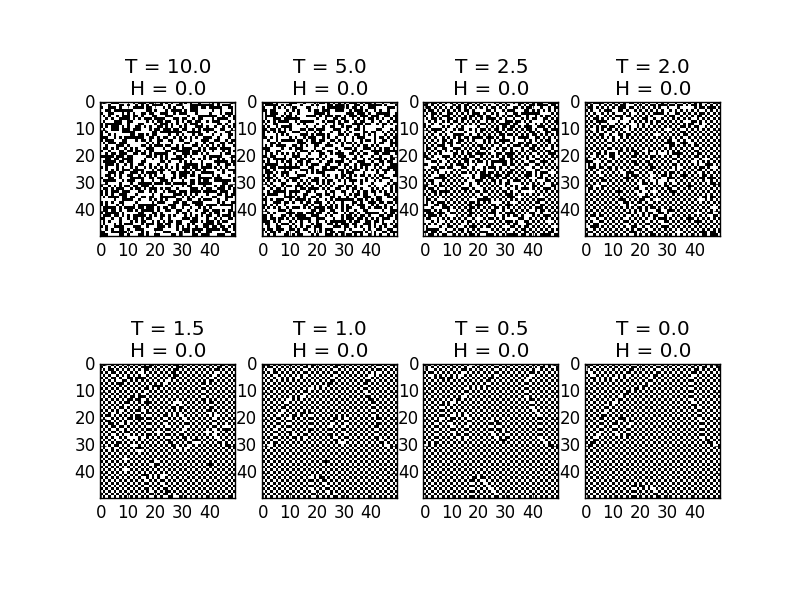
ここでは、50 x 50のサイズの結晶を用意して、温度を徐々に減少させながら前述のシュミレーションを繰り返しています。１つの温度について、「すべての原子の向きを計算する」という処理を5回づつ繰り返した結果を図示しています。黒い部分が上向きスピンで、白い部分が下向きスピンを表します。ここでは、J=1として計算しています。（図の「H=0」については後で説明します。）
温度が下がるにつれて、スピンの向きがそろった「島」が徐々に広がる様子がよく分かります。温度を下げていった際に、スピンが上向きに揃うのか下向きに揃うのかが謎でしたが、ここでは、上向きの島と下向きの島に分割されるという結果になりました。いやぁ。もっともらしいですね。
ここで、この結晶にちょっといたずらをして、すこーしだけ弱い磁場を上向きに加えてみます。先ほど、外から磁石のN極を近づける絵を描きましたが、それほど強力ではない磁石をこんな感じで近くに置いておくものと思ってください。この場合、外部の磁石の磁場をHとして、
E = - S * H
というエネルギーが余計に加わります。原子のスピン S が上向き（S=1）の方がエネルギーが小さくなることが分かります。これに応じて、先ほどの「スピンが上を向く確率」は、次のように変化します。
数学が得意な人は、ちょいと考えると、先程よりもスピンが上を向く確率 P が大きくなることに気がつくと思います。この確率の下に先ほどと同じシュミレーションをすると次のような結果になります。
H=0.5ですので、1つの原子間ペアの約半分の強さの磁場を外部から加えていることになります。この結果、温度がT=2.5あたりで一気にスピンが上向きにそろっていることが分かります。いやぁ。もっともらしいですね。
ちなみに、物質の温度を下げていくと、ある温度を堺にして、物質の性質がコロッと変わることを相転移と言います。（水が氷になるとか、電気抵抗が突然ゼロになるとか、そんなやつですね。）この例では、T=2.5あたりで、スピンの向きが揃い出すという相転移が観測されたことになります。
なお、ここで紹介したシュミレーションのコードは、こちらになります。この本で勉強した、NumPy & Pandasを使っています。
- 作者: Wes Mckinney
- 出版社/メーカー: Oreilly & Associates Inc
- 発売日: 2012/10/29
- メディア: ペーパーバック
- この商品を含むブログ (6件) を見る
機械学習とシュミレーション技法について
さて、Ising Modelの解説はここまでにして、唐突ながら、機械学習の話をしてみます。機械学習というのは、超ざっくりというと、ある観測データの集合を元にして、そのデータをうまく記述する数式を見つけ出すという手法です。見つけ出した数式を元に、まだ観測していない未知のデータを予測するなどの活用が可能です。（典型的には、メールの文面からそれがスパムである確率を計算する数式を見つけるとか、YouTubeの動画から「ネコ」が登場する動画であるか判定する数式を見つけるとか、ですね。）
この時、「適切な数式」を見つけ出す際によく出てくるのが、「最小値問題を解く」という処理です。詳細はおもいっきりぶっとばしますが、ある観測データに対して、ある計算式を最小にするようなパラメータ値を見つけると、そのパラメータ値で目的の数式が完成させられるという場面です。
しかしながら、大量の観測データを元にした「ある計算式」はとても複雑で、それを最小にするパラメータ値は、普通の計算手法では求めることができません。このような際に利用するのが、Gibbsサンプリングのような「シュミレーション技法」です。
先ほどのIsing Modelを思い出すと、それぞれの原子のスピンはエネルギーを小さくする方向に動こうとします。では、すべてのスピン間のエネルギーの合計が一番小さくなるのは、どのような状態でしょうか？ これは、エネルギーを「ある数式」とした最小値問題に他なりません。もちろん、この場合は、「すべてのスピンが同じ方向」が答えだとすぐに分かりますが、仮にまともに計算できないような複雑な問題だった場合、先ほど紹介したシュミレーションで最小値になるスピン配置を探し出すという代案が考えられます。
ただし、あくまでシュミレーションですので、必ずしも正解が得られるとは限らない点に注意が必要です。
たとえば、H=0でシュミレーションした場合、徐々に温度を下げていっても、本当の最小値を実現する配置（すべてのスピンが同じ向き）にはなりませんでした。これは、Ising Modelに限らず、このようなシュミレーションでは一般的に起こる問題です。温度を下げていくことで、エネルギーが小さくなる方向に配置が変化していることは間違いないのですが、最小値ではなく「極小値」に落ち着く可能性があるためです。
やや作為的ですが、右半分が全部上向きで、左半分が全部下向きという配置を考えます。この状態から、どれか1つだけスピンの向きを変えると、エネルギーはどうなるでしょうか？ よく考えると分かるように、境界部分を含めて、どのスピンを反転してもかならずエネルギーは上昇してしまいます。これは、この状態のエネルギーが極小値になっているということを意味します。本当の意味での最小値にするには、右半分（もしくは左半分）のスピンをまとめてエイヤッと反転する必要がありますが、1つずつ順番に変化させるというシュミレーションでは、そのような状態にたどり着くことができないわけです。
このような問題を回避して、いかにして真の最小値に近づけるかが、シュミレーション技法の研究テーマの１つとなります。
Googleの量子コンピュータについて
ところで、前述のシュミレーションの問題が生まれる原因として、「シュミレーションに使うコンピュータがパラレル処理をうまく扱えないことが悪い」と考えることはできないでしょうか？ たとえば、50 x 50 = 2500個のスピンの動きを完全に並列に計算できる特殊なコンピュータがあれば、本物の結晶の動きを正確にシュミレーションして、より正確な結果を得ることができるのではないでしょうか？
実は、Googleが発表して話題になった量子コンピュータ（D-Wave）は、このような発想に基いています。これは、量子化されたIsing Modelを計算するための専用のプロセッサーを搭載したコンピュータで、多数のスピンの状態を並列にシュミレーションすることで、より高速かつ正確にIsing Modelの最小値問題を解くことができる（と言われている）ものです。先ほどの例では、スピンは上か下かの２値しかとりませんでしたが、D-Waveでは、より多数の「量子化された」スピンの状態をシュミレーションします。
というと、
「Ising Model専用のコンピュータって意味あんの？」
という気持ちも湧いてきますが、スピン間の相互作用係数 J を複雑に変化させることで、非常に広い範囲の最小値問題が（量子化された）Ising Modelで表現できることが分かっているそうです。（先の例では、すべてのスピン間で共通の J=1 でしたが、原子ごとにJの値を変えるようなことも可能ですよね。）
ちなみに、D-Waveの解説では、「量子アニーリング」やら「焼きなまし法」やら怪しげな用語が登場しますが、これは、（おもいっきり要約すると）先ほどのシュミレーションのように高温状態から出発して、徐々に温度を下げながらシュミレーションを進めていくことで、極小値ではなく、本当の最小値に到達できるようにする技法のことです。
このぐらいの前提知識をもっておくと、（適当にググっただけですが）こんな資料とかも分かった気分になれると思います。
おまけ
さきほどのシュミレーションでは、「隣り合ったスピンは揃いたがる」という前提で計算しましたが、仮に「隣り合ったスピンは反対向きになりたがる」という前提にするとどうなるでしょうか。シュミレーションのやり方はまったく同じで、エネルギーを表す定数 J を負の値（J = -1）にすればOKです。
結果はこちら。いやぁ。もっともらしいですね。
