HeskellのMonadを圏論のMonad/Kleisli Tripleと対比する

作者: 圏論の歩き方委員会
出版社/メーカー: 日本評論社
発売日: 2015/09/09
メディア: 単行本
この商品を含むブログを見る

オフィスの机の上に新たな挑戦状（上記の本）が置いてあったので読んでみると、Kleisli tripleとMonadの関係が説明されていて、「そういえば、Kleisli tripleとMonadの同値性って、ちゃんと証明したことなかったなー」と思って書き始めたのがこのエントリーです。

いったい何の寝言を言ってるのかと思われそうですが・・・

HaskellのMonadを圏論の言葉に置き換えて理解する際に、圏論における「Kleisli triple」に対応させる方法と、圏論における「Monad」に対応させる方法があります。圏論の世界で「Kleisli triple」と「Monad」は互いに変換可能なので、どちらを用いても理論的には同じなのですが、HaskellのMonadを理解する際に、「Kleisli triple」として見る方法と「（圏論における）Monad」として見る方法を使い分けると便利なことがよくあります。というわけで、これらの関係を整理するのがこのエントリーの目標です。次の順番で解説を進めます。

(i) HaskellのMonadと圏論におけるKleisli tripleの関係
(ii) HaskellのMonadと圏論におけるMonadの関係
(iii) 圏論におけるMonadとKleisli tripleの同値性の証明

HaskellのMonadと圏論におけるKleisli tripleの関係

まず、HaskellのMonadはご存知の通り、次のMonad則を満たす演算として定義されます。

return :: A -> TA
f :: A -> B
g :: B -> C

return x >>= f == f x                       ―――(1)
m >>= return == m                           ―――(2)
(m >>= f) >>= g == m >>= (\x -> f x >>= g)  ―――(3)

ここで、圏論の記法に合わせるために、変数の型を大文字（A,B,C）、型コンストラクタをTと表記しています。

続いて、圏論におけるKleisli triple (T, η, #）は、次のように定義されます。これは、圏の種類によらずに定義できるのものですが、ここでは、Haskellとの対比を明確にするため、対象とする圏は、Haskellの変数型を「対象」、関数を「射」として定義されるものとします。

・対象Aに対して、別の対象TAを割り当てるルールTが決まっている。
・各対象Aについて、A -> TAの射 $\eta_A$ が用意されている。（ $\eta_A$ を集めた射の族をηと表記しています。）
・#は、射（A -> TB）を射（TA -> TB)に変換する写像の族である。
・ηと#は、次の法則を満たす。

　 $f^\#\circ\eta_A = f$ 　―――(1')
　 $\eta_A^\# = id_{TA}$ 　―――(2')
　 $g^\#\circ f^\# = (g^\#\circ f)^\#$ 　―――(3')

ここで、# は、

f :: A -> TB

のお尻を上げて、

f# :: TA -> TB

に変換する演算であることに注意します。

この時、次の対応関係によって、HaskellのMonadとKleisli Tripleを関連付けることができます。

・return ⇔ η
・m >>= f ⇔ $f^\#(m)$

つまり、 $\eta_A : A \longrightarrow TA$ がreturn演算子に対応しており、Monadの合成演算は、「#でfのお尻を上げてから、mを代入する」操作に対応します。

ここで、(1)〜(3)のMonad則は、(1')〜(3')の法則に対応することが分かります。

まず、上記の対応関係で、(1)をKleisli Tripleの言葉に直すと次のようになります。これは、(1')とまったく同じものです。

$(f^\#\circ\eta_A)(x) = f(x)$

(2)は、次のようになります。これは、(2')と同じです。

$\eta^\#(m) = m$

最後の(3)は次になります。これは、(3')と同じになります。

$(g^\# \circ f^\#)(m)=(g^\# \circ f)^\#(m)$

このように、Kleisli Tripleの言葉に翻訳することにより、Monadの合成（>>=）を「お尻あげ演算子 #」を使って理解（議論）することが可能になります。

HaskellのMonadと圏論におけるMonadの関係

圏論におけるMonadは、関手と自然変換を使って定義されるので、ちょっと理解が大変です・・・。（HaskellのMonadと見た目がえらい異なります。）圏論におけるMonad (T, η, μ) は、次のように定義されます。

まず、Tは、対象とする圏の自己関手とします。また、idは、恒等関手とします。

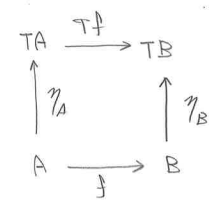
次に、ηは、id -> T の自然変換、つまり任意の射 f (A->B) に対して、次の図式を可換にする射 $\eta_A$ の族です。

$\eta_B\circ f = Tf \circ \eta_A$ 　―――(4)

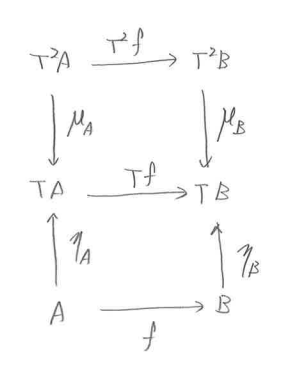
μは、T^2 -> T の自然変換、つまり任意の射 f (A->B) 対して、次の図式を可換にする射 $\mu_A$ の族です。

$\mu_B\circ T^2f = Tf \circ \mu_A$ 　―――(5)

ここで、ηは関手の皮を被せる演算であるのに対して、μは、関手の皮を一枚はがすような演算になっている事に注意します。次のようにスタックすると分かりやすくなります。

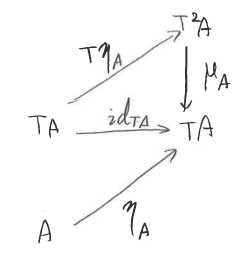
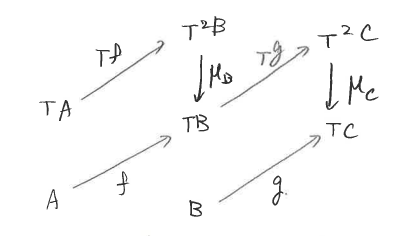
そしてさらに、これらの演算は、次の図式を可換します。

数式で表すと次のとおりです。

$\mu_A \circ \eta_{TA} = id_{TA}$ 　―――(6)
$\mu_A \circ T\eta_A = id_{TA}$ 　―――(7)
$\mu_A\circ T\mu_A = \mu_A\circ \mu_{TA}$ 　―――(8)

これで、「圏論におけるMonad」の定義は終わりです。

そして、これは、次の対応関係でHaskellのMonadと関係づけることができます。

・return ⇔ η
・m >>= f ⇔ $(\mu\circ Tf)(m)$

Monadの合成において、Kleisli tripleの場合は、fのお尻を上げて対応したのに対して、こちらでは、関手Tで、fの頭とお尻の両方を持ち上げておいて、最後にμで、関手の皮を一枚はがしています。

これらが同じ関係を表すことは、この後で証明することにして、ここではひとまず、Monad則の対応を確認しておきます。

まず、(1)は、圏論のMonadで書き直すと次のようになります。

$(\mu_{TB}\circ Tf)\circ\eta_A(x)=f(x)$

これは、(4)と(6)を使って示すことができます。

$(\mu_B\circ Tf)\circ\eta_A=\mu_B\circ(Tf\circ\eta_A)=\mu_B\circ(\eta_{TB}\circ f)$ 　（∵(4)でBをTBとした場合）
　 $=(\mu_B\circ\eta_{TB})\circ f=id_{TB}\circ f$ 　（∵(6)でAをBとした場合）
　 $=f$

(2)は、次のようになります。これは、(7)と同じことです。

$(\mu_A\circ T\eta_A)(m)=m$

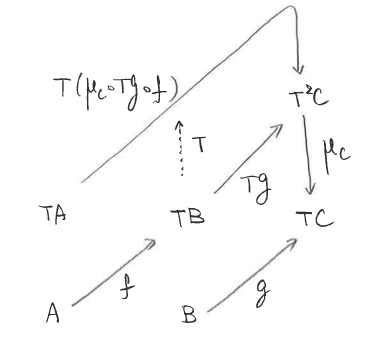
最後に(3)は、次のようになります。

$(\mu_C\circ Tg)\circ(\mu_B\circ Tf) = \mu_C\circ T(\mu_c\circ Tg\circ f)$

左辺：　　右辺：

これは、(5)と(8)を使って示すことができます。

$(\mu_C\circ Tg)\circ(\mu_B\circ Tf)=\mu_C\circ(Tg\circ\mu_B)\circ Tf=\mu_C\circ(\mu_{TC}\circ T^2g)\circ Tf$ 　（∵(5)でAをB、BとTC、fをgとした場合）
　 $=(\mu_C\circ\mu_{TC})\circ T^2g\circ Tf=(\mu_C\circ T\mu_C)\circ T^2g\circ Tf$ 　（∵(8)でAをCとした場合）
　 $= \mu_C\circ T(\mu_c\circ Tg\circ f)$ 　（∵Tは関手）