等式の束縛条件を持つ問題のDuality
束縛条件 の下に
の停留値を求める問題は、一般に、Lagrangeの未定乗数法により、
---- (1-1)
の停留値問題に帰着される。つまり、
の解を求めると、 の(束縛条件の無い)停留値と
の(束縛条件のある)停留値が一致する。
ここで、 を固定して、
についての停留値
を先に求めて、
に再代入したものをdual function
として定義する。
この時、dual functionの停留値を求めることと、元々のLangrangeanの停留値を求めることは同じになる。なぜなら、
より、
つまり、(1-1)の(束縛条件を持たない)停留値問題の解を として、次の関係(Strong Duality)が成り立つ。
・ ----- (1-2)
・ は、元々の(束縛条件を持つ)停留値問題の解でもある。
・ は、dual function
の停留値問題の解でもある。
不等式の束縛条件を持つ問題のDuality
束縛条件 の下に
の最小値を求める問題を考える。
まず、形式的に次のLagrangeanを定義する。
これが、について下に凸で最小値を持つ範囲の
に対して、次のようにdual functionを定義する。
この時、任意のに対して次の不等式が成り立つ。
---- (2-1)
(は、束縛条件下の最小値問題の解なので、
)
従って、仮に、
---- (2-2)
を満たすが存在する場合、もともとの最小値問題の解は、次の最大値問題を解くことに帰着する。
このは、(2-1)の不等式をすべて等式にするので、
つまり、
これから、次も成り立つことが分かる。
ここで、(2-2)を満たす の存在を示す。
元々の条件付き最小値問題の解は、束縛条件を満たす領域に存在するが、束縛条件は次の2つに分類される。
: Activeな束縛条件
: Inactiveな束縛条件
Inactiveな束縛条件は、 の近傍では、
を束縛しないことに注意すると、Inactiveな束縛条件に対して
とおいた、
の停留値問題の解として、 (および、Activeな束縛条件に対する
)は決定される。さらに、この(等式の束縛条件を持つ)停留値問題のdual functionについて、(1-2)が成り立つので、次が得られる(Inactiveな束縛条件に対しては、
とおく)。
については、次のように示せる。
したがって、
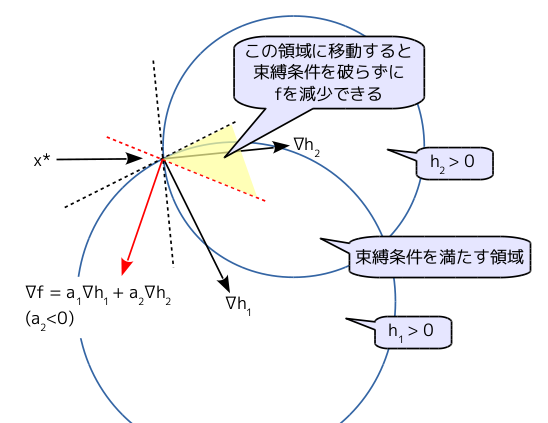
この時、下図より、 となるものが存在すると、束縛条件を満たす方向に
を移動して
の値を小さくすることができるので、
が最小値問題の解であることに矛盾する。
※ここで、Slater Condition を仮定している。
まとめ
以上の議論に含まれていた各種条件を整理すると、次のようにまとめられる。
束縛条件 の下に
の最小値を求める問題を考える。
この時、Lagrangeanとdual functionを次のように定義する。
(定義域は、
について下に凸で最小値を持つ範囲の
)
ここで、dual functionの最大値問題の解を とする。
この時、次の関係が成立する。
・
・
・
・
※最後の等式は、Activeな束縛条件については で、Inactiveな束縛条件については、
となることから成立する。