こちらです。
# -*- coding: utf-8 -*- # # Perceptronによる二項分類 # # 2015/04/24 ver1.0 # import numpy as np import matplotlib.pyplot as plt import pandas as pd from pandas import Series, DataFrame from numpy.random import multivariate_normal #------------# # Parameters # #------------# N1 = 30 # クラス t=1 のデータ数 Mu1 = [0,0] # クラス t=1 の中心座標 N2 = 20 # クラス t=-1 のデータ数 Mu2 = [15,10] # クラス t=-1 の中心座標 Variances = [20,25] # 両クラス共通の分散(2種類の分散で計算を実施) # データセット {x_n,y_n,type_n} を用意 def prepare_dataset(variance): cov1 = np.array([[variance,0],[0,variance]]) cov2 = np.array([[variance,0],[0,variance]]) df1 = DataFrame(multivariate_normal(Mu1,cov1,N1),columns=['x','y']) df1['type'] = 1 df2 = DataFrame(multivariate_normal(Mu2,cov2,N2),columns=['x','y']) df2['type'] = -1 df = pd.concat([df1,df2],ignore_index=True) df = df.reindex(np.random.permutation(df.index)).reset_index() return df[['x','y','type']] # Perceptronのアルゴリズム(確率的勾配降下法)を実行 def run_simulation(variance, data_graph, param_graph): tset = prepare_dataset(variance) tset1 = tset[tset['type']==1] tset2 = tset[tset['type']==-1] ymin, ymax = tset.y.min()-5, tset.y.max()+10 xmin, xmax = tset.x.min()-5, tset.x.max()+10 data_graph.set_ylim([ymin-1, ymax+1]) data_graph.set_xlim([xmin-1, xmax+1]) data_graph.scatter(tset1.x, tset1.y, marker='o') data_graph.scatter(tset2.x, tset2.y, marker='x') # パラメータの初期値とbias項の設定 w0 = w1 = w2 = 0.1 bias = 0.5 * (tset.x.mean() + tset.y.mean()) # Iterationを30回実施 paramhist = DataFrame([[w0,w1,w2]], columns=['w0','w1','w2']) for i in range(30): for index, point in tset.iterrows(): x, y, type = point.x, point.y, point.type if type * (w0*bias + w1*x + w2*y) < 0: w0 += type * 1 w1 += type * x w2 += type * y paramhist = paramhist.append( Series([w0,w1,w2], ['w0','w1','w2']), ignore_index=True) # 判定誤差の計算 err = 0 for index, point in tset.iterrows(): x, y, type = point.x, point.y, point.type if type * (w0*bias + w1*x + w2*y) < 0: err += 1 err_rate = err * 100 / len(tset) # 結果の表示 linex = np.arange(xmin-5, xmax+5) liney = - linex * w1 / w2 - bias * w0 / w2 label = "ERR %.2f%%" % err_rate data_graph.plot(linex,liney,label=label,color='red') data_graph.legend(loc=1) paramhist.plot(ax=param_graph) param_graph.legend(loc=1) # Main if __name__ == '__main__': fig = plt.figure() # 2種類の分散で実行 for c, variance in enumerate(Variances): subplots1 = fig.add_subplot(2,2,c+1) subplots2 = fig.add_subplot(2,2,c+2+1) run_simulation(variance, subplots1, subplots2) fig.show()
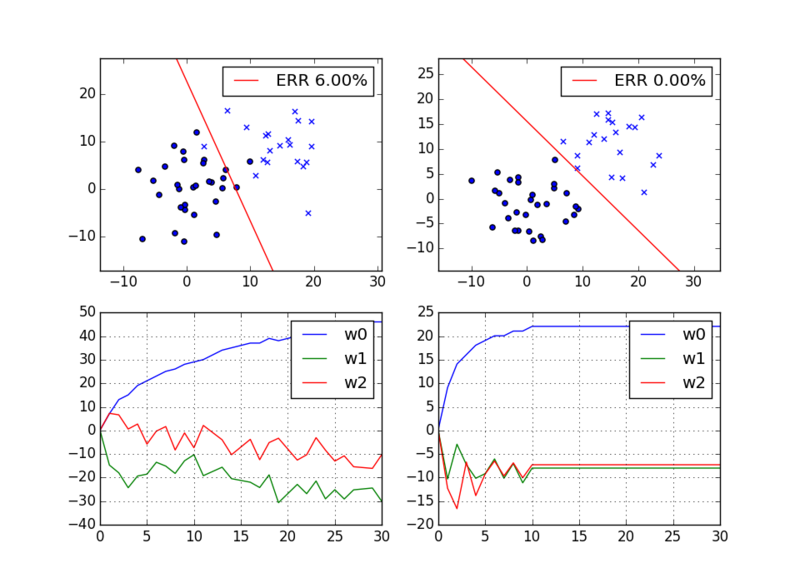
実行結果は次のようになります。左右に二種類の結果が出ています。
完全に分離できる場合は、パラメータは収束していますが、完全に分離できない場合は収束せずに変動を繰り返すことが分かります。