2016-09-09

Kernel PCA (Principal Component Analysis) の導出

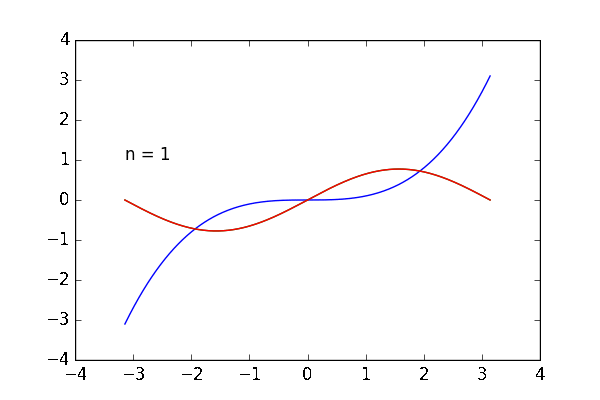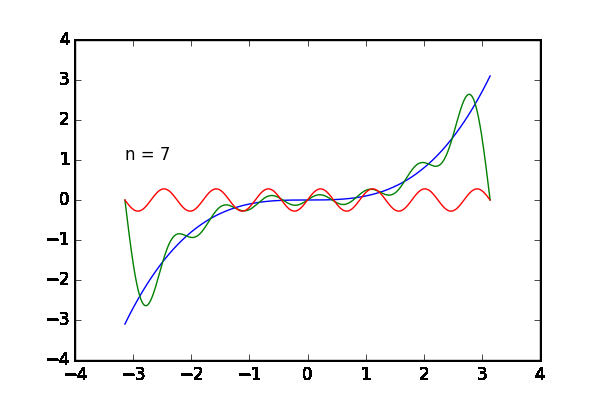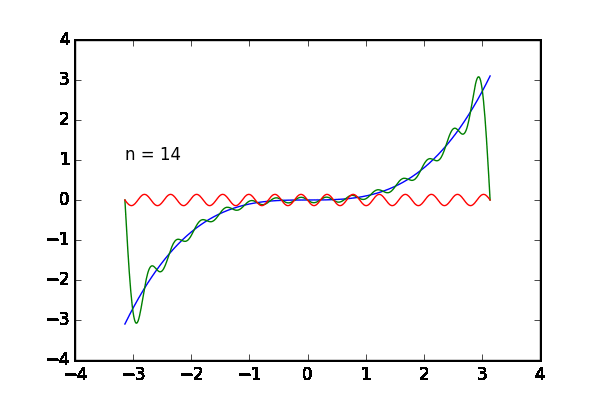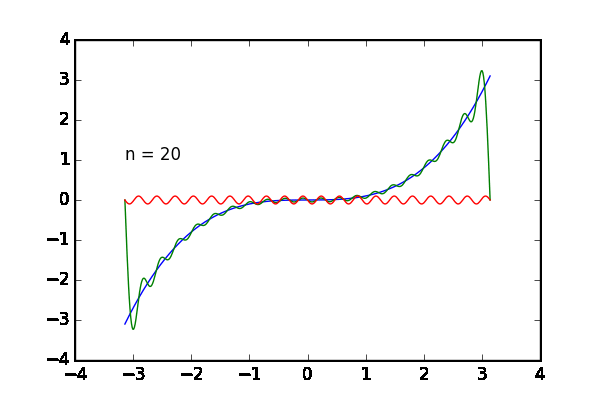
何の話かというと

Python Machine Learning: Unlock deeper insights into Machine Leaning with this vital guide to cutting-edge predictive analytics (English Edition)

作者:Raschka, Sebastian
Packt Publishing

Amazon

この本のKernel PCAの説明が相当に計算を端折っていて、これは読者もつらいだろぅ。。。と思って途中の計算を端折らずになるべく正確に導出してみました。

※実対称行列の固有値分解とLagrangeの未定乗数法は前提知識とします。

普通のPCA

はじめに、Kernelを使わない普通のPCAを導出します。

データセット $\{{\mathbf x}_n\}_{n=1}^N,\,\,{\mathbf x}_n \in {\mathbf R}^{\rm D}$ の分散共分散行列を ${\mathbf S}$ とします。この時、 ${\mathbf S}$ は正定値の実対称行列より、正（もしくは0）の固有値を持つ、互いに直行する固有ベクトルで固有値分解されます。この点に注意すると、第1主軸（その方向の成分の分散が最大になる方向）を ${\mathbf u}_1\,\,(\|{\mathbf u}_1\|=1)$ とする時、これは、最大固有値を持つ固有ベクトルに一致することが次のように示されます。

次に、第2主軸（ ${\mathbf u_1}$ に直行する方向で、その方向の成分の分散が最大になる方向） ${\mathbf u}_2\,\,(\|{\mathbf u}_2\|=1)$ は、2番目に大きな固有値を持つ固有ベクトル、さらに第3主軸（ ${\mathbf u_1}$ と ${\mathbf u_2}$ の両方に直行する方向で、その方向の成分の分散が最大になる方向） ${\mathbf u}_3\,\,(\|{\mathbf u}_3\|=1)$ は、3番目に大きな固有値を持つ固有ベクトル・・・であることが帰納的に証明されます。

Kernel PCA

D次元空間のデータに対して、何らかの非線形関数 ${\mathbf \phi}({\mathbf x}) \in {\mathbf R}^M\,\,(M>D)$ を用いて、M次元空間のデータに変換した後、データセット $\{ {\mathbf \phi}({\mathbf x_n}) \}_{n=1}^N$ に対して、M次元空間上でのPCAを適用します。すると、次のような結論が得られます。（証明は後ほど掲載）

========
$k({\mathbf x_n},{\mathbf x_{n'}})={\mathbf \phi}({\mathbf x}_n)^{\rm T}{\mathbf \phi}({\mathbf x}_{n'})\,\,(n,n'=1,\cdots,N)$ を成分とする対称行列を ${\mathbf K}\in {\mathbf R}^N\times{\mathbf R}^N$ とする時、グラム行列 $\tilde{\mathbf K}$ を次式で定義する。

　 $\tilde{\mathbf K} = {\mathbf K} - {\mathbf 1}_N{\mathbf K} - {\mathbf K}{\mathbf 1}_N + {\mathbf 1}_N{\mathbf K}{\mathbf 1}_N$

ここに、 ${\mathbf 1}_N$ は、すべての成分が $1/N$ という値のN✕N行列である。

$\tilde{\mathbf K}$ の正の固有値について、大きい方から並べたものを $\lambda_1,\lambda_2,\cdots$ 、対応する（大きさ1の）固有ベクトルを ${\mathbf u}_1,{\mathbf u}_2,\cdots \in {\mathbf R}^N$ とする時、第i主軸方向の単位ベクトルは、次式で与えられる。

　 ${\mathbf v}_i =\frac{1}{\sqrt{\lambda_i N}} \sum_{n=1}^N u_{in}\left\{{\mathbf \phi}({\mathbf x}_n)-\frac{1}{N}\sum_{n'=1}^N{\mathbf \phi}({\mathbf x}_{n'})\right\}$

この時、任意の点 ${\mathbf x}$ について、非線形変換されたM次元空間における第i主軸成分は、次で計算される。

　 ${\mathbf \phi}({\mathbf x})^{\rm T}{\mathbf v}_i = \frac{1}{\sqrt{\lambda_i N}} \sum_{n=1}^N u_{in}k({\mathbf x},{\mathbf x}_n)$

ここに、 $k({\mathbf x},{\mathbf x}')={\mathbf \phi}({\mathbf x})^{\rm T}{\mathbf \phi}({\mathbf x}')$ をカーネル関数と呼ぶ。
========

この結果の重要なポイントして、 ${\mathbf u}_i$ の定義、および、最後の計算式を用いれば、非線形変換 ${\mathbf \phi}({\mathbf x})$ の具体的な形がわからなくても、カーネル関数 $k({\mathbf x},{\mathbf x}')$ が与えられれば、第i主軸成分が計算できることが挙げられます。

たとえば、カーネル関数として、ガウスカーネル $k({\mathbf x},{\mathbf x}_n)=\exp \left\{-\gamma(\| {\mathbf x}-{\mathbf x}_n \|^2)\right\}$ を用いた場合を考えます。これは、 $u_{in}$ が大きな値を取る $n$ について、 ${\mathbf x_n}$ との距離が近いほど、その主軸成分が大きくなることを意味します。つまり、k近傍法のように「どのデータとの距離が近いかによって、主軸成分の大小が決まる」ことになります。これによって、元の ${\mathbf x}$ 平面上でのデータの配置に関係なく、それぞれのデータとの距離を特徴量として抽出できることを意味します。（ガウスカーネルに対応するような ${\mathbf \phi}({\mathbf x})$ が存在することは別途証明が必要ですが、その証明はここでは省略します。）

それでは、前述の結論の証明です。

Kernel PCAの適用例

三日月形に並んだデータ群について、第1〜第4主軸成分の等高線を描きます。赤色は値が大きい所（山）で、青色は値が小さい所（谷）を示します。

gist.github.com

第1主軸成分を見ると、2つの三日月のどちらのデータに近いかで成分の大小が決まっていることが分かります。さらに第2主軸成分は、それぞれの三日月を左右に分割しています。高次の主軸成分になるほど、より細かくデータを分割することが観察できます。

2016-08-30

「[改訂新版] プロのためのLinuxシステム構築・運用技術」が発売されます

www.amazon.co.jp

2010年12月に初版が発行された「プロのための Linuxシステム構築・運用技術」の改訂新版が発売されることになりました。2016年9月20日に販売開始予定です。改訂作業にあたりご協力いただいた皆様に改めてお礼を申し上げます。

本書の前付けより、「改訂にあたり」を掲載させていただきます。

改訂にあたり

　「はじめに」の日付にもある通り、本書の初版は2010年に出版されました。それから約6年の歳月を経て、改訂版を出版させていただくことになりました。対象とするLinuxディストリビューションは、Red Hat Enterprise Linux 5（RHEL5）から、Red Hat Enterprise Linux 7（RHEL7）へと変わり、各種のツールやコマンドは新しいものへと置き換わりました。しかしながら、6年前に書いた「はじめに」を読み返すと、驚くべきことに、その内容はまったく古くなってはいないようです。パブリッククラウドの活用が広がり、物理サーバーに一からOSをインストールする機会は減りました。コンテナ技術を活用して、OSの存在を意識することなく、手軽にアプリケーションをデプロイできるようになりました。Linuxサーバーを活用する上で必要となるOSの知識は、どんどん減っているかのようにも感じられます。その結果 ―― 思わぬ「落とし穴」にはまる機会が大きく増えました。
　誰でも手軽にLinuxサーバーが活用できるようになった今こそ、ストレージ、ネットワーク、そして、内部構造を含めた「OSの全体像」を把握することが、何よりも求められています。Linuxを専門とする方々はもちろんのこと、Linuxを基礎から勉強しようと思いながら、そのきっかけがなかった皆さんに、最新バージョンのRed Hat Enterprise Linuxに対応した本書をお届けしたいと思います。改訂版の執筆にあたり、「はじめに」に加えて、本書末の「おわりに」、そして、本文中のコラムについては、用語の表記をのぞいて、あえて初版の内容のままにしてあります。Unix/Linuxの世界で受けつがれる、今も変わらない「本質」の存在を感じていただければ幸いです。