PRML Figure5.11を再現するコード

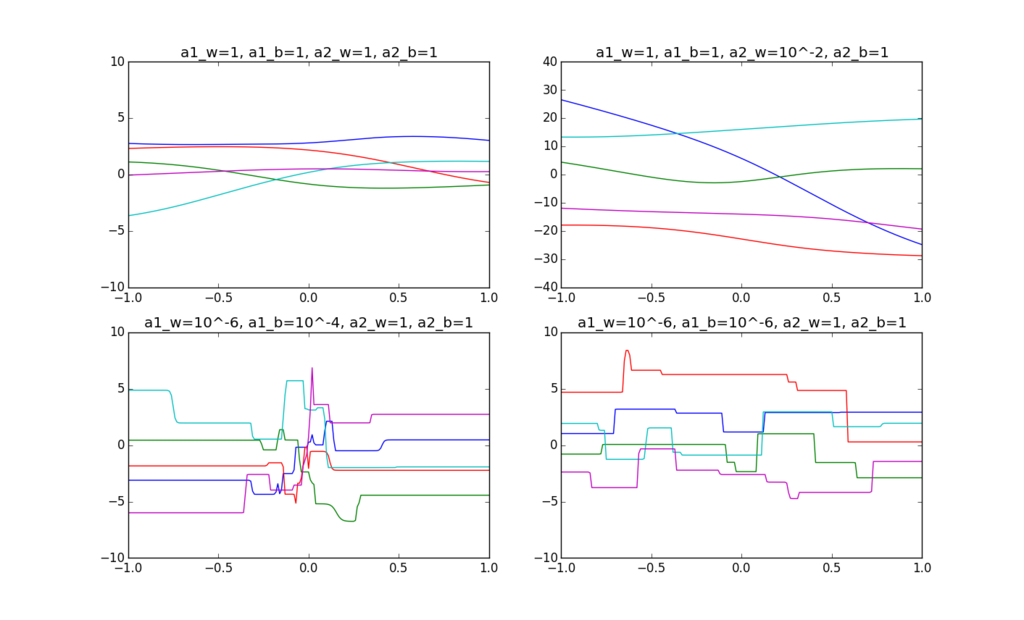
これ

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from numpy.random import normal

alpha1_w = [1.0, 1.0,    10**-6, 10**-6]
alpha1_b = [1.0, 1.0,    10**-4, 10**-6]
alpha2_w = [1.0, 10**-2, 1.0,    1.0]
alpha2_b = [1.0, 1.0,    1.0,    1.0]

titles = [ 'a1_w=1, a1_b=1, a2_w=1, a2_b=1',
           'a1_w=1, a1_b=1, a2_w=10^-2, a2_b=1',
           'a1_w=10^-6, a1_b=10^-4, a2_w=1, a2_b=1',
           'a1_w=10^-6, a1_b=10^-6, a2_w=1, a2_b=1']

yrange = [10,40,10,10]

class NN:
    def __init__(self, n, m):
        self.m = m  # number of hidden units
        self.n = n  # number of inputs
        w = {}      # w[('layer', ('unit', 'order'))]
        for j in range(1,m+1):
            for k in range(n+1):
                w[(1,(j,k))] = 0
        for j in range(m+1):
            w[(2,(1,j))] = 0
        self.w = w

    def sigmoid(self, a):
        return 1.0/(1.0+np.exp(-a))

    def f(self, x):
        m = self.m
        w = self.w
        a = [0.0]*(m+1) # input to hidden units
        z = [0.0]*(m+1) # output from hidden units
        for j in range(1,m+1):
            a[j] = w[(1,(j,0))]*1.0
            for k in range(1, self.n+1):
                a[j] += w[(1,(j,k))]*x[k-1]
            z[j] = np.tanh(a[j])
        a_k = w[(2,(1,0))]*1.0
        for j in range(1, m+1):
            a_k += w[(2,(1,j))]*z[j] # final output
        return a_k

def run_simulation(m, subplot, i):
    a1_w = alpha1_w[i]
    a1_b = alpha1_b[i]
    a2_w = alpha2_w[i]
    a2_b = alpha2_b[i]

    nn = NN(1,m)

    for c in range(5):
        for j in range(1,m+1):
            nn.w[(1,(j,0))] = normal(loc=0,scale=1.0/np.sqrt(a1_b))
            nn.w[(1,(j,1))] = normal(loc=0,scale=1.0/np.sqrt(a1_w))

        nn.w[(2,(1,0))] = normal(loc=0,scale=1.0/np.sqrt(a2_b))
        for j in range(1,m+1):
            nn.w[(2,(1,j))] = normal(loc=0,scale=1.0/np.sqrt(a2_w))

        subplot.set_title(titles[i])
        subplot.set_xlim([-1, 1])
        subplot.set_ylim([-yrange[i], yrange[i]])
        linex = np.arange(-1,1.01,0.01)
        subplot.plot(linex, nn.f(np.array([linex])))

# main
if __name__ == '__main__':
    fig = plt.figure()
    for i in range(4):
        subplot = fig.add_subplot(2,2,i+1)
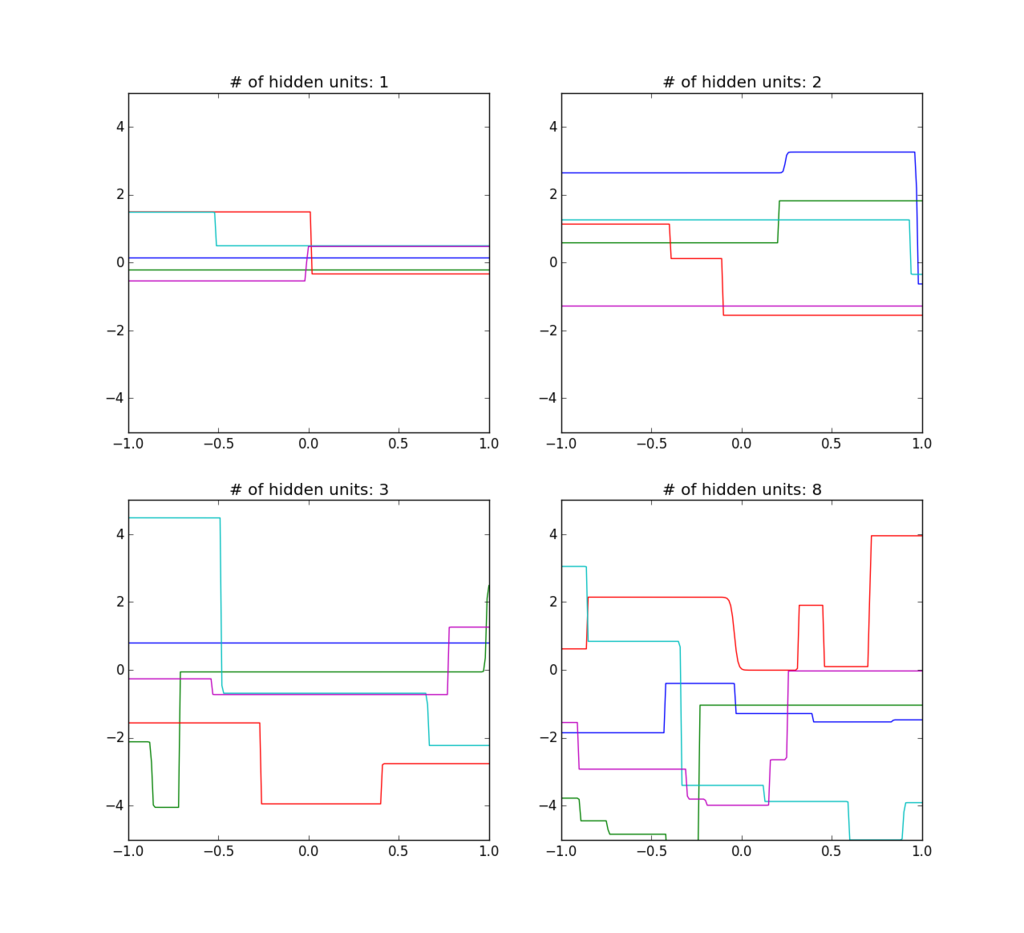
        run_simulation(12, subplot, i)
    fig.show()